
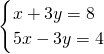
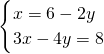

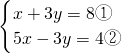 ,
, ;
;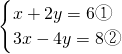 ,
,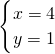 ;
;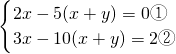 ,
, ,
,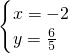 ;
;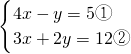 ,
,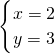 ;
;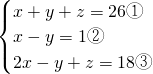 ,
,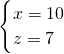 ,
, .
.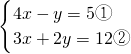 ,然后用加减消元法求出x,再利用代入法求出y;
,然后用加减消元法求出x,再利用代入法求出y;

科目:初中数学 来源: 题型:解答题
 写为小数即
写为小数即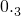 ,反之,无限循环小数
,反之,无限循环小数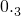 写成分数即
写成分数即 .一般地,任何一个无限循环小数都可以写成分数形式.现在就以
.一般地,任何一个无限循环小数都可以写成分数形式.现在就以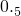 为例进行讨论:设:
为例进行讨论:设: ,由:
,由: …,得:x=0.5555…,10x=5.555…,于是:10x-x=5.555…-0.555…=5,即:10x-x=5,解方程得:
…,得:x=0.5555…,10x=5.555…,于是:10x-x=5.555…-0.555…=5,即:10x-x=5,解方程得: ,于是得:
,于是得: .请仿照上述例题完成下列各题:
.请仿照上述例题完成下列各题: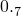 写成分数,即
写成分数,即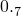 =______.
=______. 为分数吗?请完成你的探究过程.
为分数吗?请完成你的探究过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com