
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
分析 先根据题意得出A、B两点的坐标,进而可得出结论.
解答 解:∵点A、B分别是函数y=$\frac{4}{x}$(x>0)和y=-$\frac{4}{x}$(x<0)图象上的一点,A、B两点的横坐标分别为a、b,
∴A(a,$\frac{4}{a}$),B(b,-$\frac{4}{b}$)且a>0,b<0.
∵OA=OB,a+b≠0,
∴a=-$\frac{4}{b}$,b=-$\frac{4}{a}$
∴ab=$\frac{4}{b}$•$\frac{4}{a}$=$\frac{16}{ab}$,
∴ab=-4.
故选A.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:填空题
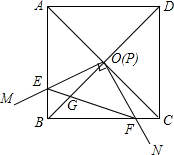 如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是(1),(2),(3),(5).
如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是(1),(2),(3),(5).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视,正在播放《大国工匠》 | |
| B. | 袋中只有10个球,且都是红球,任意摸出一个球是红球 | |
| C. | 5年后数学课代表会考上清华大学 | |
| D. | 2015年全年由367天 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{2}$=2 | B. | $\sqrt{3}$-$\sqrt{3}$=0 | C. | $\sqrt{2}$×$\sqrt{2}$=4 | D. | $\sqrt{(-3)^{2}}$=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
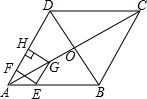 如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒查看答案和解析>>
科目:初中数学 来源: 题型:解答题
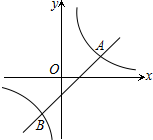 如图,已知A(4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点
如图,已知A(4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
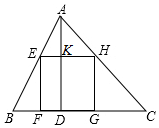 若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为ha,hb,hc,各边上的内接正方形的边长分别记为xa,xb,xc
若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为ha,hb,hc,各边上的内接正方形的边长分别记为xa,xb,xc查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-4,3) | B. | (-3,-4) | C. | (-3,4) | D. | (3,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com