(1)已知一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1、x2,则x1=______,x
2=______;x1+x2=______;x1x2=______.
(2)应用(1)的结论解答下列问题:已知x1、x2是关于x的方程x2-4kx+4=0的两个实数根,且满足:x12+x22-6(x1+x2)=-8.求k、x1、x2的值.
解:(1)根据一元二次方程的求根公式与根与系数的关系可得:x
1=
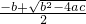
,x
2=
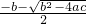
,
x
1+x
2=-

,x
1x
2=

.
(2)由(1)可得:x
1x
2=

=4,x
1+x
2=4k;
x
12+x
22-6(x
1+x
2)=-8可化简为(x
1+x
2)
2-2x
1x
2-6(x
1+x
2)=-8,
代入可得:16k
2-8-6×4k=-8;
解可得k
1=0(舍去),k
2=

,
故x
1=3+

,x
2=3-

.
分析:(1)根据一元二次方程的求根公式与根与系数的关系可得答案;
(2)由(1)可得x
1、x
2的值与其间的关系,x
12+x
22-6(x
1+x
2)=-8可化简为(x
1+x
2)
2-2x
1x
2-6(x
1+x
2)=-8,解可得k的值,进而可得x
1、x
2的值.
点评:主要考查了根的判别式和根与系数的关系.要掌握根与系数的关系式:x
1+x
2=-

,x
1x
2=

.把所求的代数式变形成x
1+x
2,x
1x
2的形式再整体代入是常用的方法之一.

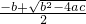 ,x2=
,x2=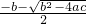 ,
, ,x1x2=
,x1x2= .
. =4,x1+x2=4k;
=4,x1+x2=4k; ,
, ,x2=3-
,x2=3- .
. ,x1x2=
,x1x2= .把所求的代数式变形成x1+x2,x1x2的形式再整体代入是常用的方法之一.
.把所求的代数式变形成x1+x2,x1x2的形式再整体代入是常用的方法之一. 
