
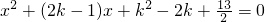 ①
①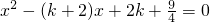 ②
② )=4k-25≥0,
)=4k-25≥0, ,
, )≥0,
)≥0, ,
, ,则方程②有实数根;
,则方程②有实数根; ,
,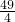 =0,即(x-
=0,即(x- )2=0,
)2=0, ;
; =0,
=0, =7,
=7,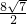
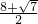 ,x2=
,x2=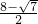 .
. )=4k-25≥0,则有k≥
)=4k-25≥0,则有k≥ ;△2=(k+2)2-4(2k+
;△2=(k+2)2-4(2k+ )≥0,则k≥5或k≤-1,由于方程①、②都有实数根,于是有k≥
)≥0,则k≥5或k≤-1,由于方程①、②都有实数根,于是有k≥ ,则k的最小整数值为7;
,则k的最小整数值为7; ,则若方程①和②中只有一个方程有实数根;则方程①和②中只有一个方程有实数根,只有方程②有实数根,方程①不一定实数根;
,则若方程①和②中只有一个方程有实数根;则方程①和②中只有一个方程有实数根,只有方程②有实数根,方程①不一定实数根; ,得到k=5或6,然后把它们分别代入方程,利用因式分解法或求根公式法解方程即可.
,得到k=5或6,然后把它们分别代入方程,利用因式分解法或求根公式法解方程即可.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
| k |
| 2 |
1-
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 13 |
| 2 |
| 9 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的两个一元二次方程:
方程①:  ; 方程②:
; 方程②:  .
.
(1)若方程①有两个相等的实数根,求解方程②;
(2)若方程①和②中只有一个方程有实数根, 请说明此时哪个方程没有实数根, 并化
简![]() ;
;
(3)若方程①和②有一个公共根a, 求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市海淀区九年级上学期期中测评数学卷 题型:解答题
已知关于x的两个一元二次方程:
方程①:  ; 方程②:
; 方程②:  .
.
(1)若方程①有两个相等的实数根,求解方程②;
(2)若方程①和②中只有一个方程有实数根, 请说明此时哪个方程没有实数根, 并化
简 ;
;
(3)若方程①和②有一个公共根a, 求代数式 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2012届北京市海淀区九年级上学期期中测评数学卷 题型:解答题
已知关于x的两个一元二次方程:
方程①:  ; 方程②:
; 方程②:  .
.
(1)若方程①有两个相等的实数根,求解方程②;
(2)若方程①和②中只有一个方程有实数根, 请说明此时哪个方程没有实数根, 并化
简 ;
;
(3)若方程①和②有一个公共根a, 求代数式 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com