
使得函数值为零的自变量的值称为函数的零点。例如,对于函数 ,令y=0,可得x=1,我们就说1是函数
,令y=0,可得x=1,我们就说1是函数 的零点。 己知函数
的零点。 己知函数 (
( m为常数)。
m为常数)。

(1)当 =0时,求该函数的零点;
=0时,求该函数的零点;
(2)证明:无论 取何值,该函数总有两个零点;
取何值,该函数总有两个零点;
(3)设函数的两个零点分别为 和
和 ,且
,且 ,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线
,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。
(1)当 =0时,该函数的零点为
=0时,该函数的零点为 和
和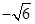 。 ……………………………2分
。 ……………………………2分
(2)令y=0,得△=
∴无论 取何值,方程
取何值,方程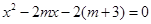 总有两个不相等的实数根。
总有两个不相等的实数根。
即无论 取何值,该函数总有两个零点。
………………………………6分
取何值,该函数总有两个零点。
………………………………6分
(3)依题意有 ,
,
由 解得
解得 。
。
∴函数的解析式为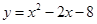 。
………………………………8分
。
………………………………8分
令y=0,解得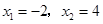
∴A( ),B(4,0)
),B(4,0)
作点B关于直线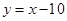 的对称点B’,连结AB’,
的对称点B’,连结AB’,
则AB’与直线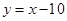 的交点就是满足条件的M点。 ………………………………10分
的交点就是满足条件的M点。 ………………………………10分
易求得直线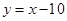 与x轴、y轴的交点分别为C(10,0),D(0,10)。
与x轴、y轴的交点分别为C(10,0),D(0,10)。
连结CB’,则∠BCD=45°
∴BC=CB’=6,∠B’CD=∠BCD=45°
∴∠BCB’=90°
即B’( )
………………………………12分
)
………………………………12分
设直线AB’的解析式为 ,则
,则
 ,解得
,解得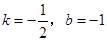
∴直线AB’的解析式为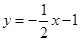 ,
,
即AM的解析式为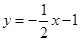 。
………………………………14分
。
………………………………14分
【解析】(1)根据题中给出的函数的零点的定义,将m=0代入y=x2-2mx-2(m+3),然后令y=0即可解得函数的零点;
(2)令y=0,函数变为一元二次方程,要想证明方程有两个解,只需证明△>0即可;
(3)根据题中条件求出函数解析式进而求得A、B两点坐标,个、作点B关于直线y=x-10的对称点B′,连接AB′,求出点B′的坐标即可求得当MA+MB最小时,直线AM的函数解析式


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012届山东东阿县第三中学中考模拟数学试卷(带解析) 题型:解答题
使得函数值为零的自变量的值称为函数的零点.例如,对于函数 ,令
,令 ,可得
,可得 ,我们就说
,我们就说 是函数
是函数 的零点.请根据零点的定义解决下列问题:已知函数
的零点.请根据零点的定义解决下列问题:已知函数 (m为常数).
(m为常数).
【小题1】当m=0时,求该函数的零点
【小题2】证明:无论m取何值,该函数总有两个零点;
【小题3】设函数的两个零点分别为 和
和 ,且
,且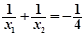 ,此时函数图象与
,此时函数图象与 轴的交点分别为A、B(点A在点B左侧),点M在直线
轴的交点分别为A、B(点A在点B左侧),点M在直线 上,当MA+MB最小时,求直线AM的函数解析式.
上,当MA+MB最小时,求直线AM的函数解析式.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖南长沙卷)数学 题型:解答题
使得函数值为零的自变量的值称为函数的零点。例如,对于函数 ,令y=0,可得x=1,我们就说1是函数
,令y=0,可得x=1,我们就说1是函数 的零点。
的零点。
己知函数 (
( m为常数)。
m为常数)。
(1)当 =0时,求该函数的零点;
=0时,求该函数的零点;
(2)证明:无论 取何值,该函数总有两个零点;
取何值,该函数总有两个零点;
(3)设函数的两个零点分别为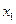 和
和 ,且
,且 ,此时函数图象与x轴的交点分
,此时函数图象与x轴的交点分
别为A、B(点A在点B左侧),点M在直线 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建厦门外国语学校九年级中考模拟数学试卷(解析版) 题型:解答题
使得函数值为零的自变量的值称为函数的零点.例如,对于函数 ,令
,令 ,可得
,可得 ,我们就说
,我们就说 是函数
是函数 的零点.请根据零点的定义解决下列问题:已知函数
的零点.请根据零点的定义解决下列问题:已知函数 (k为常数).当k=2时,求该函数的零点;
(k为常数).当k=2时,求该函数的零点;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com