
 已知:如图正△ABC的边长为2,正△DEF的边长为1,点D与A重合,E在AB上,F在AC上,把正△DEF按边AB→BC→CA无滑动地滚动,始终保持D、E、F三点在△ABC的边上或内部,直到△DEF回到初始位置,则D经过的最短路程为
已知:如图正△ABC的边长为2,正△DEF的边长为1,点D与A重合,E在AB上,F在AC上,把正△DEF按边AB→BC→CA无滑动地滚动,始终保持D、E、F三点在△ABC的边上或内部,直到△DEF回到初始位置,则D经过的最短路程为| 2 |
| 3 |
| 2 |
| 3 |
科目:初中数学 来源:同步练习数学九年级下册(北师大版) 题型:044
(1)已知:如图,△ABC为正三角形,点M为BC边上任意一点,点N为CA边上任意一点,且BM=CN,BN与AM相交于Q.试求∠BQM的度数.

(2)如果将上图中的正三角形改为正方形ABCD(如下图),点M为BC边上任意一点,点N为CD边上任意一点,且BM=CN,BN与AM相交于Q.那么∠BQM等于多少度呢?试说明理由.

(3)如果将(1)中的正三角形改为正五边形…正n边形,其余条件都不变,请据(1)(2)的求解思路,将你推断的结论填入下表:(注:正多边形的各个内角都相等)

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
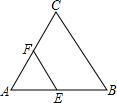 已知:如图正△ABC的边长为2,正△DEF的边长为1,点D与A重合,E在AB上,F在AC上,把正△DEF按边AB→BC→CA无滑动地滚动,始终保持D、E、F三点在△ABC的边上或内部,直到△DEF回到初始位置,则D经过的最短路程为________.
已知:如图正△ABC的边长为2,正△DEF的边长为1,点D与A重合,E在AB上,F在AC上,把正△DEF按边AB→BC→CA无滑动地滚动,始终保持D、E、F三点在△ABC的边上或内部,直到△DEF回到初始位置,则D经过的最短路程为________.查看答案和解析>>
科目:初中数学 来源:《24.3 正多边形与圆》2009年同步练习(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com