Question

（本小题满分8分）
已知，在△ABC中，∠BAC=90°，AB=AC，BC=，点D、E在BC边上（均不与点B、C重合，点D始终在点E左侧），且∠DAE＝45°．
【小题1】（1）请在图①中找出两对相似但不全等的三角形，写在横线上      ，       ；
【小题2】（2）设BE＝m，CD＝n，求m与n的函数关系式，并写出自变量n的取值范围；
【小题3】（3）如图②，当BE＝CD时，求DE的长；
【小题4】（4）求证：无论BE与CD是否相等，都有DE²=BD²+CE².

Answer 1

【小题1】解：（1）△ADE∽△BAE，△ADE∽△CDA，△BAE∽△CDA；（写出任意两对即可）
【小题2】（2）∵∠BAC＝90°，AB＝AC，BC＝，
由（1）知△BAE∽△CDA，
∴.
∴. ∴ （）
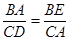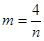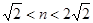【小题3】（3）由（2）只BE·CD＝4，
∴BE＝CD＝2.
∴BD＝BC－CD＝.
∴DE＝BE－BD＝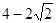
【小题4】（4）如图，依题意，可以将△AEC绕点A顺时针旋转90°至△AFB的位置，
则FB＝CE，AF＝AE，∠1＝∠2，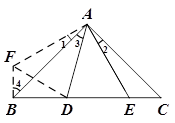
∴∠FBD＝90°.
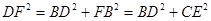∴. ……………6分
∵∠3＋∠1＝∠3＋∠2＝45°，
∴∠FAD＝∠DAE.
又∵AD＝AD，AF＝AE，
∴△AFD≌△AED.
∴DE＝DF. ………………………………………………………………………7分
∴

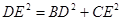
解析