练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．36°40′30″化成用度表示的形式36.675°．

    分析 根据小单位化成大单位除以进率，可得答案．

    解答 解：36°40′30″=36°40.5′=36.675°，
    故答案为：36.675°．

    点评 本题考查了度分秒的换算，利用小单位化成大单位除以进率是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．如图，正方形ABCD中，点E、F分别在AD、CD上，且AE=DF，连接BE、AF，相交于G．求证：AF⊥BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，网格中的小方格均是边长为1的正方形，△ABC的顶点与点O均在格点上（每个小正方形的顶点叫格点）．

    （1）以点B为旋转中心，将△ABC按逆时针方向旋转90°后得到△A1BC1，画出△A1BC1；
    （2）以点O为旋转中心，将△ABC按顺时针方向旋转180°后得到△A2B2C2，画出△A2B2C2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．一元一次不等式2x-3≥-1的解集在数轴上表示为（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

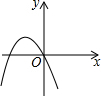    4．二次函数y=ax2+bx+c（a≠0）的图象如图所示，那么一次函数y=bx+c与反比例函数y=$\frac{a}{x}$在同一平面直角坐标系中的图象大致是（　　）
    A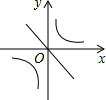．B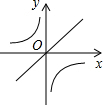．C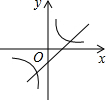．D．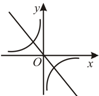

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，将△ABC沿着过AB中点D的直线折叠，使点A落在BC边上的A1处，称为第1次操作，折痕DE到BC的距离记为h1，还原纸片后，再将△ADE沿着过AD中点D1的直线折叠，使点A落在DE边上的A2处，称为第2次操作，折痕D1E1到BC的距离记为h2；按上述方法不断操作下去…，经过第2017次操作后得到的折痕D2016E2016，到BC的距离记为h2017；若h1=1，则h2017的值为2-$\frac{1}{{2}^{2016}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．宏兴企业接到一批产品的生产任务，按要求必须在14天内完成．已知每件产品的出厂价为60元．工人甲第x天生产的产品数量为y件，y与x满足如下关系：y=$\left\{\begin{array}{l}7.5x（{0≤x≤4}）\\ 5x+10（{4＜x≤14}）\end{array}$．
    （1）工人甲第几天生产的产品数量为70件？
    （2）设第x天生产的产品成本为P元/件，P与x的函数图象如图．工人甲第x天创造的利润为W元，求W与x的函数关系式，并求出第几天时，利润最大，最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

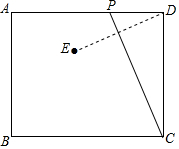    18．如图，已知矩形ABCD中，AB=4，AD=m，动点P从点D出发，在边DA上以每秒1个单位的速度向点A运动，连接CP，作点D关于直线PC的对称点E，设点P的运动时间为t（s）．
    （1）若m=6，求当P，E，B三点在同一直线上时对应的t的值．
    （2）已知m满足：在动点P从点D到点A的整个运动过程中，有且只有一个时刻t，使点E到直线BC的距离等于3，求所有这样的m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

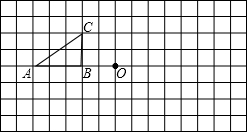
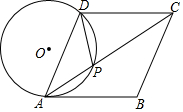    19．如图，在菱形ABCD中，点P在对角线AC上，且PA=PD，⊙O是△PAD的外接圆．
    （1）求证：AB是⊙O的切线；
    （2）若AC=8，tan∠BAC=$\frac{{\sqrt{2}}}{2}$，求⊙O的半径．

    查看答案和解析>>

    同步练习册答案