
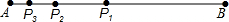 勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则APn的长度是________.
勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则APn的长度是________. )n
)n AB=
AB= ,则AP1=1-
,则AP1=1- =
= ,同理得到AP2=
,同理得到AP2= ×
× =(
=( )2,AP3=(
)2,AP3=( )3,根据此规律得到APn=(
)3,根据此规律得到APn=( )n.
)n. AB=
AB= ,
, =
= ,
, ×
× =(
=( )2,
)2, )3,
)3, )n.
)n. )n.
)n. AB≈0.618AB,并且线段AB的黄金分割点有两个.
AB≈0.618AB,并且线段AB的黄金分割点有两个. 

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com