
分析 (1)设组装A型号简易板房x套,则组装B型号简易板房(50-x)套,列出不等式组,求出整数解即可解决问题.
(2)设总组装费用为W,则W=200x+180=20x+9000,利用一次函数的性质即可解决问题.
解答 解:(1)设组装A型号简易板房x套,则组装B型号简易板房套,
根据题意得出:8x+5(50-x)≤349 ①
4x+9(50-x)≤295 ②
由①②解得:31≤x≤33,
故该公司组装A、B两种型号的简易板房时,共有3种组装方案:
组装A型号简易板房31套,则组装B型号简易板房19套,
组装A型号简易板房32套,则组装B型号简易板房18套,
组装A型号简易板房33套,则组装B型号简易板房17套;
(2)设总组装费用为W,则W=200x+180=20x+9000,
∵20>0,∴W随x的增大而增大,
当x=31时,W最小=20×31+9000=9620(元).此时x=31,50-31=19,
答:最少总组装费用是9620元,总组装费用最少时的组装方案为:组装A型号简易板房31套,则组装B型号简易板房19套.
点评 本题考查一次函数的性质、一元一次不等式组等知识,解题的关键是理解题意,学会构建不等式组或一次函数解决实际问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 遗爱湖公园的亲水平台修建了许多台阶(如图所示),春季湖水上涨后有一部分在水下.如果点C的坐标为(-1,1),D点的坐标为(0,2).(点C、D分别在第3、4级)
遗爱湖公园的亲水平台修建了许多台阶(如图所示),春季湖水上涨后有一部分在水下.如果点C的坐标为(-1,1),D点的坐标为(0,2).(点C、D分别在第3、4级)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
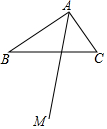 如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.
如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
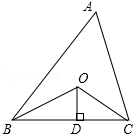 如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是$\frac{40}{3}$.
如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是$\frac{40}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | -9 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com