
 学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.
学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.分析 (按买3个A种魔方和买4个B种魔方钱数相同解答)
(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个,根据“购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购进A种魔方m个(0<m≤50),总价格为w元,则购进B种魔方(100-m)个,根据两种活动方案即可得出w活动一、w活动二关于m的函数关系式,再分别令w活动一<w活动二、w活动一=w活动二和w活动一>w活动二,解出m的取值范围,此题得解.
(按购买3个A种魔方和4个B种魔方需要130元解答)
(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个,根据“购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购进A种魔方m个(0<m≤50),总价格为w元,则购进B种魔方(100-m)个,根据两种活动方案即可得出w活动一、w活动二关于m的函数关系式,再分别令w活动一<w活动二、w活动一=w活动二和w活动一>w活动二,解出m的取值范围,此题得解.
解答 (按买3个A种魔方和买4个B种魔方钱数相同解答)
解:(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个,
根据题意得:$\left\{\begin{array}{l}{2x+6y=130}\\{3x=4y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=15}\end{array}\right.$.
答:A种魔方的单价为20元/个,B种魔方的单价为15元/个.
(2)设购进A种魔方m个(0<m≤50),总价格为w元,则购进B种魔方(100-m)个,
根据题意得:w活动一=20m×0.8+15(100-m)×0.4=10m+600;
w活动二=20m+15(100-m-m)=-10m+1500.
当w活动一<w活动二时,有10m+600<-10m+1500,
解得:m<45;
当w活动一=w活动二时,有10m+600=-10m+1500,
解得:m=45;
当w活动一>w活动二时,有10m+600>-10m+1500,
解得:45<m≤50.
综上所述:当m<45时,选择活动一购买魔方更实惠;当m=45时,选择两种活动费用相同;当m>45时,选择活动二购买魔方更实惠.
(按购买3个A种魔方和4个B种魔方需要130元解答)
解:(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个,
根据题意得:$\left\{\begin{array}{l}{2x+6y=130}\\{3x+4y=130}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=26}\\{y=13}\end{array}\right.$.
答:A种魔方的单价为26元/个,B种魔方的单价为13元/个.
(2)设购进A种魔方m个(0<m≤50),总价格为w元,则购进B种魔方(100-m)个,
根据题意得:w活动一=26m×0.8+13(100-m)×0.4=15.6m+520;
w活动二=26m+13(100-m-m)=1300.
当w活动一<w活动二时,有15.6m+520<1300,
解得:m<50;
当w活动一=w活动二时,有15.6m+520=1300,
解得:m=50;
当w活动一>w活动二时,有15.6m+520>1300,
不等式无解.
综上所述:当0<m<50时,选择活动一购买魔方更实惠;当m=50时,选择两种活动费用相同.
点评 本题考查了二元一次方程组的应用、一次函数的应用、解一元一次不等式以及解一元一次方程,解题的关键是:(1)找准等量关系,列出关于x、y的二元一次方程组;(2)根据两种活动方案找出w活动一、w活动二关于m的函数关系式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 有1对或2对 | B. | 只有1对 | C. | 只有2对 | D. | 有2对或3对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
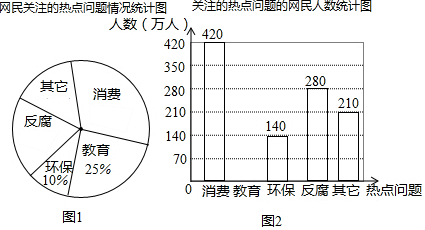
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
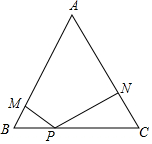 在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.
在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
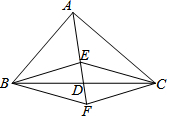 如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )
如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )| A. | EB⊥EC | B. | AB⊥AC | C. | AB=AC | D. | BF∥CE |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com