
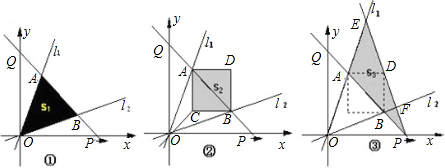
 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)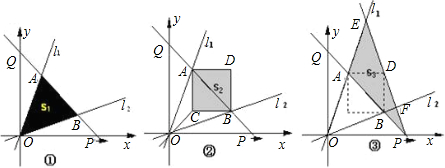
 ,解得
,解得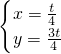 ,
, ,
,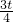 )
)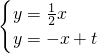 ,解得
,解得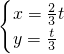
 ,
,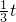 ).
). t2
t2 ,
, ).
). =
=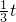 ,
, ,
, x.
x. t-
t-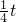 =
= ,
,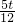 )2=
)2=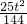 .
. t,
t,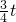 ),
),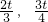 )代入得
)代入得 ,
,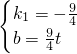
 x+
x+ t.
t.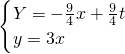 ,
,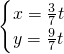
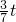 ,
,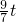 )
) t•
t•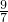 t-
t- t•
t• t=
t=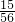 t2.
t2. t,
t,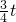 ),又P(t,0),可求直线PD解析式,从而可求点E的坐标,用S3=S△OEP-S△OAP可表示面积.
),又P(t,0),可求直线PD解析式,从而可求点E的坐标,用S3=S△OEP-S△OAP可表示面积.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•滨州)根据要求,解答下列问题:
(2013•滨州)根据要求,解答下列问题:| 1 | 5 |
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《二次函数》(08)(解析版) 题型:解答题
 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)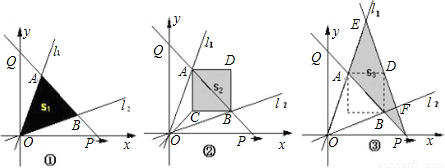
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com