
分析 (1)根据题意可知m大于0,进而求出抛物线的对称轴以及顶点坐标和点C的坐标,结合△OCP的面积为$\frac{3}{2}$即可求出m的值;
(2)设P点坐标为(1,a),直线BC的解析式为y=kx-3,直线BC与对称轴交点为D(1,n),进而求出直线BC与对称轴的交点D的坐标,结合△PBC的面积为2即可求出a的值.
解答 解:(1)根据题意可知m>0,
∵y=mx2-2mx+m-4,
∴y=m(x-1)2-4,
∴抛物线对称轴x=1,顶点坐标为(1,-4),点C坐标为(0,m-4),
∵△OCP的面积为$\frac{3}{2}$,
∴$\frac{1}{2}$×(4-m)×1=$\frac{3}{2}$,
∴m=1;
(2)设P点坐标为(1,a),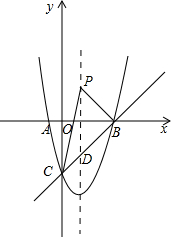
∵m=1,
∴y=mx2-2mx+m-4=x2-2x-3,
∴点A坐标为(-1,0)B(3,0),C(0,-3),
设直线BC的解析式为y=kx-3,直线BC与对称轴交点为D(1,n),
把点B(3,0)代入可得k=1,
∴直线BC的解析式为y=x-3,
∵D(1,n)在直线BC上,
∴n=1-3=-2,
∴D点坐标为(1,-2),
∴PD=|a+2|,
∵△PBC的面积为2,
∴$\frac{1}{2}$×|a+2|×3=2,
∴a=-$\frac{2}{3}$或-$\frac{10}{3}$,
∴P点坐标为(1,-$\frac{2}{3}$)或(1,-$\frac{10}{3}$).
点评 本题主要考查令抛物线与x轴交点的知识,解答本题的关键是求出抛物线的解析式,此题涉及求三角形的面积用分割法求解较简单,此题难度一般.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
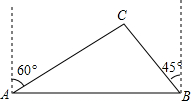 去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2.732km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?($\sqrt{3}$≈1.732)
去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2.732km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?($\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
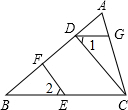 如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
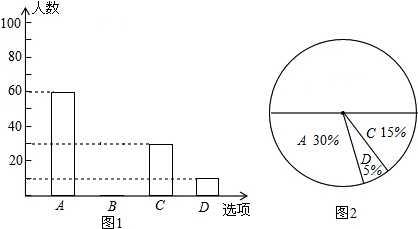
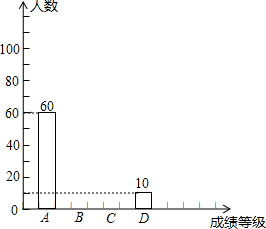 为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:
为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 占抽查学生总数的百分比 | 30% | 50% | 15% | m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
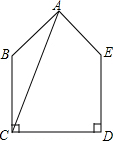 如图,面积为72的五边形ABCDE中,BC=DE=7,CD=8,∠BCD=∠EDC=90°,连接对角线AC,则AC+AE的最小值为17.
如图,面积为72的五边形ABCDE中,BC=DE=7,CD=8,∠BCD=∠EDC=90°,连接对角线AC,则AC+AE的最小值为17.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com