
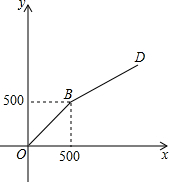
 “六一”儿童节期间,甲、乙两家网店以同样价格销售相同的儿童用品,他们的优惠方案分别为:甲店,一次性购物超过100元后的价格部分打七折;乙店,一次性购物超过500元后的价格部分打五折.设商品原价为x元,购物应付金额为y元.
“六一”儿童节期间,甲、乙两家网店以同样价格销售相同的儿童用品,他们的优惠方案分别为:甲店,一次性购物超过100元后的价格部分打七折;乙店,一次性购物超过500元后的价格部分打五折.设商品原价为x元,购物应付金额为y元.分析 (1)分0≤x≤100及x>100两种情况,找出y1与x之间的函数解析式;
(2)画出函数图象,分0≤x≤500及x>500两种情况,找出y2与x之间的函数解析式,结合两函数的解析式即可求出交点A、C的坐标;
(3)观察函数图象结合点A、C的横坐标可得出,当100<x<1100时,y1的函数图象在y2的函数图象的下方,由此即可得出结论.
解答 解:(1)当0≤x≤100时,y1=x;
当x>100时,y1=100+$\frac{7}{10}$(x-100)=0.7x+30.
∴在甲店购物时y1与x之间的函数解析式为y1=$\left\{\begin{array}{l}{x(0≤x≤100)}\\{0.7x+30(x>100)}\end{array}\right.$.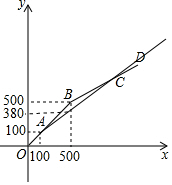
(2)画出函数图象,如图所示.
当0≤x≤500时,y2=x;
当x>500时,y1=500+$\frac{5}{10}$(x-500)=0.5x+250.
令0.7x+30=x,解得:x=100;
令0.7x+30=0.5x+220,解得:x=1100.
∴点A的坐标为(100,100),点C的坐标为(1100,800).
(3)∵当100<x<1100时,y1的函数图象在y2的函数图象的下方,
∴当购物商品原价为980元时,选择甲家网店购物更优惠.
故答案为:甲.
点评 本题考查了一次函数的应用,解题的关键是:(1)根据数量关系找出函数关系式;(2)画出函数图象;(3)根据两函数图象的上下位置关系,找出结论.


科目:初中数学 来源: 题型:解答题
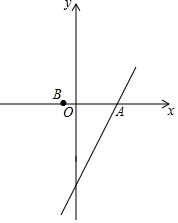 已知抛物线y1=a(x-x1)(x-x2)(a≠0,x1≠x2)与x轴分别交于A(x1,0)、
已知抛物线y1=a(x-x1)(x-x2)(a≠0,x1≠x2)与x轴分别交于A(x1,0)、查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)已知二次函数y1=-(x+1)2+4的图象如图所示,请在同一坐标系中画出二次函数y1=-(x-2)2+1的图象.
(1)已知二次函数y1=-(x+1)2+4的图象如图所示,请在同一坐标系中画出二次函数y1=-(x-2)2+1的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
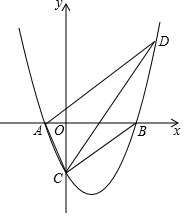 已知抛物线y=ax2+bx-3a与x轴交于A(-1,0),B(x2,0),与y轴负半轴交于点C,OB=OC.
已知抛物线y=ax2+bx-3a与x轴交于A(-1,0),B(x2,0),与y轴负半轴交于点C,OB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32,42,52 | B. | $\sqrt{2}$,$\sqrt{2}$,2 | C. | 2,3,4 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com