
 的图像,那么下列结论错误的是 ( )
的图像,那么下列结论错误的是 ( ) 
A.当 时, 时, > > ; ; | B.当 时, 时,  ; ; |
C.当 < < 时, 时, 随 随 的增大而增大; 的增大而增大; | D.上述抛物线可由抛物线 平移得到 平移得到 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
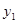 (吨)与月份
(吨)与月份 (
(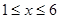 ,且
,且 取整数)之间满足的函数关系如下表:
取整数)之间满足的函数关系如下表:月份 (月) (月) | 1 | 2 | 3 | 4 | 5 | 6 |
输送的污水量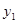 (吨) (吨) | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
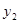 (吨)与月份
(吨)与月份 (
(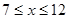 ,且
,且 取整数)之间满足二次函数关系式
取整数)之间满足二次函数关系式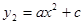 ,其图象如图所示.1至6月,污水厂处理每吨污水的费用
,其图象如图所示.1至6月,污水厂处理每吨污水的费用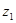 (元)与月份
(元)与月份 之间满足函数关系式
之间满足函数关系式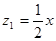 ,该企业自身处理每吨污水的费用
,该企业自身处理每吨污水的费用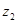 (元)与月份
(元)与月份 之间满足函数关系式
之间满足函数关系式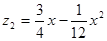 ;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.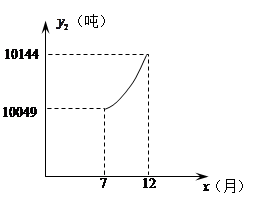
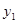 ,
,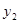 与
与 之间的函数关系式;
之间的函数关系式; 月用于污水处理的费用为W(元),试求出W与
月用于污水处理的费用为W(元),试求出W与 之间的函数关系式;
之间的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
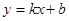 交x轴于点A(-1,0),交y轴于B点,
交x轴于点A(-1,0),交y轴于B点,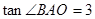 ;过A、B两点的抛物线交x轴于另一点C(3,0).
;过A、B两点的抛物线交x轴于另一点C(3,0).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象上,过点B作
的图象上,过点B作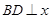 轴,垂足为D,且B点横坐标为
轴,垂足为D,且B点横坐标为 .
.
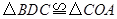 ;
;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com