
 解得
解得 ,
, .
. 分别代入方程x2-(k-2)x+2k=0中,
分别代入方程x2-(k-2)x+2k=0中, 时原方程可化为x2+
时原方程可化为x2+ x+
x+ =0,解得x=-
=0,解得x=- 或x=-1(不合题意舍去).
或x=-1(不合题意舍去). ,
,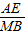 =
= ,即
,即 =
= ----②,
----②, .
. =
= =4.
=4.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2000年全国中考数学试题汇编《图形的相似》(02)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2000年全国中考数学试题汇编《圆》(05)(解析版) 题型:解答题
 ;
;
查看答案和解析>>
科目:初中数学 来源:2000年全国中考数学试题汇编《圆》(02)(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2010年四川省泸州市泸县九年级数学自我评价练习题(二)(解析版) 题型:解答题
 ;
;
查看答案和解析>>
科目:初中数学 来源:2000年浙江省金华市中考数学试卷(解析版) 题型:填空题
 (2000•金华)如图,要测量河两岸相对的两点A、B间的距离,先从B处出发,与AB成90°角方向,向前走50米到C处立一根标杆,然后方向不变继续朝前走10米到D处,在D处沿垂直于BD的方向再走5米到达E处,使A(目标物),C(标杆)与E在同一直线上,则AB的长为 米.
(2000•金华)如图,要测量河两岸相对的两点A、B间的距离,先从B处出发,与AB成90°角方向,向前走50米到C处立一根标杆,然后方向不变继续朝前走10米到D处,在D处沿垂直于BD的方向再走5米到达E处,使A(目标物),C(标杆)与E在同一直线上,则AB的长为 米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com