
 如图,过y轴上任意一点P,作x轴的平分线,分别于反比例函数y=$\frac{4}{x}$和y=$\frac{2}{x}$的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为3.
如图,过y轴上任意一点P,作x轴的平分线,分别于反比例函数y=$\frac{4}{x}$和y=$\frac{2}{x}$的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为3. 分析 先设P(0,b),由直线AB∥x轴,则A,B两点的纵坐标都为b,而A,B分别在反比例函数y=-$\frac{4}{x}$和y=$\frac{2}{x}$的图象上,可得到A点坐标为(-$\frac{4}{b}$,b),B点坐标为($\frac{2}{b}$,b),从而求出AB的长,然后根据三角形的面积公式计算即可.
解答 解:设P(0,b),
∵直线AB∥x轴,
∴A,B两点的纵坐标都为b,而点A在反比例函数y=-$\frac{4}{x}$的图象上,
∴当y=b,x=-$\frac{4}{b}$,即A点坐标为(-$\frac{4}{b}$,b),
又∵点B在反比例函数y=$\frac{2}{x}$的图象上,
∴当y=b,x=$\frac{2}{b}$,即B点坐标为($\frac{2}{b}$,b),
∴AB=$\frac{2}{b}$-(-$\frac{4}{b}$)=$\frac{6}{b}$,
∴S△ABC=$\frac{1}{2}$•AB•OP=$\frac{1}{2}$•$\frac{6}{b}$•b=3.
故答案为:3.
点评 本题考查的是反比例函数系数k的几何意义,即在反比例函数y=$\frac{k}{x}$的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且BD=3AD.那么AE:AC等于( )
如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且BD=3AD.那么AE:AC等于( )| A. | 2:3 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-3)2+7 | B. | y=(x+3)2+7 | C. | y=(x-3)2-7 | D. | y=(x+3)2-7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
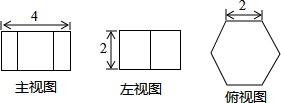 如图是某几何体的三视图,则该几何体的表面积为( )
如图是某几何体的三视图,则该几何体的表面积为( )| A. | 16+6$\sqrt{3}$ | B. | 16+12$\sqrt{3}$ | C. | 24+6$\sqrt{3}$ | D. | 24+12$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 酒驾猛于虎,但很多人不以为是,为了加强人们对酒驾危害的认识,交警部门加大了对酒驾的检查力度.某市交警在2015年2月28日这天对本市各大主要交通路口进行车辆检查,如图,AC是该市解放路的一段,AE,BF,CD都是南北方向的街道,与解放路AC的交叉路口分别是A,B,C.已知出警点D位于点A的北偏东45°方向、点B的北偏东30°方向上,BD=2km,∠DBC=30°.
酒驾猛于虎,但很多人不以为是,为了加强人们对酒驾危害的认识,交警部门加大了对酒驾的检查力度.某市交警在2015年2月28日这天对本市各大主要交通路口进行车辆检查,如图,AC是该市解放路的一段,AE,BF,CD都是南北方向的街道,与解放路AC的交叉路口分别是A,B,C.已知出警点D位于点A的北偏东45°方向、点B的北偏东30°方向上,BD=2km,∠DBC=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com