
| A. | ②③ | B. | ①②④ | C. | ③④ | D. | ②③④ |
分析 利用二元一次方程的解及方程组的解定义判断即可.
解答 解:已知关于x、y的方程组$\left\{\begin{array}{l}{x+y=1-a}\\{x-y=3a+5}\end{array}$(a≥0),解得:$\left\{\begin{array}{l}{x=a+3}\\{y=-2a-4}\end{array}\right.$,给出下列说法:
①当a=1时,方程组的解也是方程x+y=0的一个解,不符合题意;
②当x-2y=a+3+4a+8>8时,a>-$\frac{3}{5}$,不符合题意;
③不论a取什么实数,2x+y=2的值始终不变,符合题意;
④某直角三角形的两条直角边长分别为x+y=-a-1,x-y=3a+7,则其面积最大值为$\frac{8}{3}$,符合题意.
故选C
点评 此题考查了二元一次方程组的解,二元一次方程的解,方程组的解即为能使方程组中两方程都成立的未知数的值.


科目:初中数学 来源: 题型:选择题
 如图,在直角坐标系中,点A、B分别在x轴,y轴上,点A的坐标为(-2,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=2$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为( )
如图,在直角坐标系中,点A、B分别在x轴,y轴上,点A的坐标为(-2,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=2$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为( )| A. | 6 | B. | 6+2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
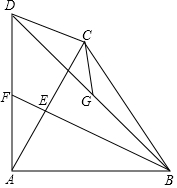 如图,在四边形ABCD中,AB=AD,AB⊥AD.连接AC、BD,AC⊥DC.过点B作BE⊥AC,分别交AC、AD于点E、F.点G为BD中点,连接CG.
如图,在四边形ABCD中,AB=AD,AB⊥AD.连接AC、BD,AC⊥DC.过点B作BE⊥AC,分别交AC、AD于点E、F.点G为BD中点,连接CG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
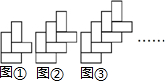 用长为2cm、宽为1cm的矩形无缝隙的摆出如图所示的图形,图形①由4个矩形组成,其外轮廓(即图形的周长)为14cm,图形②由6个矩形组成,图形③由8个矩形组成…以此类推,则图形⑨的外轮廓为46cm.
用长为2cm、宽为1cm的矩形无缝隙的摆出如图所示的图形,图形①由4个矩形组成,其外轮廓(即图形的周长)为14cm,图形②由6个矩形组成,图形③由8个矩形组成…以此类推,则图形⑨的外轮廓为46cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com