考点:正方形的性质,一次函数图象上点的坐标特征
专题:规律型
分析:首先求得直线的解析式,分别求得A1,A2,A3…的坐标,可以得到一定的规律,分别求得B1,B2,B3…的坐标,可以得到一定的规律,据此即可求解.
解答:
解:∵B
1的坐标为(1,1),点B
2的坐标为(3,2),
∴正方形A
1B
1C
1O
1边长为1,正方形A
2B
2C
2C
1边长为2,
∴A
1的坐标是(0,1),A
2的坐标是:(1,2),
代入y=kx+b得
,
解得:
,
则直线的解析式是:y=x+1.
∵A
1B
1=1,点B
2的坐标为(3,2),
∴A
1的纵坐标是:1=2
0,A
1的横坐标是:0=2
0-1,
∴A
2的纵坐标是:1+1=2
1,A
2的横坐标是:1=2
1-1,
∴A
3的纵坐标是:2+2=4=2
2,A
3的横坐标是:1+2=3=2
2-1,
∴A
4的纵坐标是:4+4=8=2
3,A
4的横坐标是:1+2+4=7=2
3-1,
∴A
n的纵坐标是:2
n-1,横坐标是:2
n-1-1.
∴点A
n的坐标为 (2
n-1-1,2
n-1).
∵点B
1的坐标为(1,1),点B
2的坐标为(3,2),
∴点B
3的坐标为(7,4),
∴Bn的横坐标是:2
n-1,纵坐标是:2
n-1.
∴B
n的坐标是(2
n-1,2
n-1).
故答案为:(2
n-1-1,2
n-1),(2
n-1,2
n-1).
点评:本题主要考查的是正方形的性质,熟知待定系数法求函数解析式和坐标的变化规律,正确得到点的坐标的规律是解题的关键.

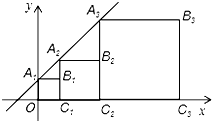 在直角坐标系中,正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…、AnBnCnCn-1按如图所示的方式放置,其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上,点C1、C2、C3、…、Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为
在直角坐标系中,正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…、AnBnCnCn-1按如图所示的方式放置,其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上,点C1、C2、C3、…、Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为 解:∵B1的坐标为(1,1),点B2的坐标为(3,2),
解:∵B1的坐标为(1,1),点B2的坐标为(3,2),

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案 已知:如图DE∥BC,且∠1=∠3,试说明:FG∥DC.(请把下列解题过程补充完整并在括号中注明理由)
已知:如图DE∥BC,且∠1=∠3,试说明:FG∥DC.(请把下列解题过程补充完整并在括号中注明理由)