解:(1)解法一:由题意得,x
1x
2=m-2<0.
解得,m<2.
∵m为正整数,
∴m=1.
∴y=x
2-1.
解法二:由题意知,当x=0时,y=0
2+(m-1)×0+(m-2)<0.
(以下同解法一)
解法三:∵△=(m-1)
2-4(m-2)=(m-3)
2,
∴x=
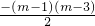
,
∴x
1=-1,x
2=2-m.
又∵x
1x
2<0,
∴x
2=2-m>0.
∴m<2.
(以下同解法一.)
解法四:令y=0,即x
2+(m-1)x+(m-2)=0,
∴(x+1)(x+m-2)=0
∴x
1=-1,x
2=2-m.
(以下同解法三.)
(2)解法一:∵x
1<1,x
2>1,
∴x
1-1<0,x
2-1>0.
∴(x
1-1)(x
2-1)<0,
即x
1x
2-(x
1+x
2)+1<0.
∵x
1+x
2=-(m-1),x
1x
2=m-2,
∴(m-2)+(m-1)+1<0.
解得m<1.
∴m的取值范围是m<1.
解法二:由题意知,当x=1时,
y=1+(m-1)+(m-2)<0.
解得:m<1.
∴m的取值范围是m<1.
解法三:由(Ⅰ)的解法三、四知,x
1=-1,x
2=2-m.
∵x
1<1,x
2>1,
∴2-m>1,
∴m<1.
∴m的取值范围是m<1.
(3)存在.
解法一:因为过A,B两点的圆与y轴相切于点C(0,2),
所以A,B两点在y轴的同侧,
∴x
1x
2>0.
由切割线定理知,OC
2=OA•OB,
即2
2=|x
1||x
2|.
∴|x
1x
2|=4
∴x
1x
2=4.
∴m-2=4.
∴m=6.
解法二:连接O'B,O'C.
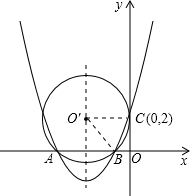
圆心所在直线
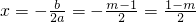
,
设直线
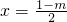
与x轴交于点D,圆心为O',
则O'D=OC=2,O'C=OD=
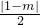
.
∵AB=|x
2-x
1|=
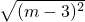
=|m-3|,BD=

,
∴
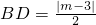
.
在Rt△O′DB中,
O'D
2+DB
2=O'B
2.
即
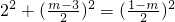
.
解得m=6.
(4)设P(x
1,y
1),Q(x
2,y
2),
则y
1=x
12-1,y
2=x
22-1.
过P,Q分别向x轴引垂线,垂足分别为P
1(x
1,0),Q(x
2,0).
则PP
1∥FO∥QQ
1.
所以由平行线分线段成比例定理知,
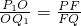
.
因此,
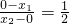
,即x
2=-2x
1.
过P,Q分别向y轴引垂线,垂足分别为P
2(0,y
1),Q
2(0,y
2),
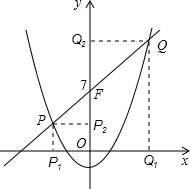
则PP
2∥QQ
2.所以△FP
2P∽△FQ
2Q.
∴
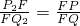
.
∴
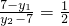
.
∴21-2y
1=y
2.
∴21-2(x
12-1)=x
22-1
∴23-2x
12=4x
12-1
∴x
12=4,
∴x
1=2,或x
1=-2.
当x
1=2时,点P(2,3).
∵直线l过P(2,3),F(0,7),
∴
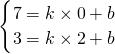
,
解得
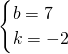
当x
1=-2时,点P(-2,3).
∵直线l过P(-2,3),F(0,7),
∴
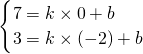
,
解得
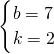
故所求直线l的解析式为:y=2x+7,或y=-2x+7.
分析:(1)本题有多种解法.首先由题意可得x
1x
2=m-2<0,可求出m值,然后根据题意求出解析式即可.
(2)已知题意x
1<1,x
2>1推出(x
1-1)(x
2-1)<0,然后可知x
1+x
2=-(m-1),x
1x
2=m-2,代入等式可解.
(3)存在.根据题意因为过A,B两点的圆与y轴相切于点C(0,2),所以A,B两点在y轴的同侧,故x
1x
2>0,
再根据圆的切割线定理得知OC
2=OA•OB.
(4)首先分别假设P.Q的坐标为(x
1,y
1),(x
2,y
2).由平行线定理求出x
2与x
1的等量关系.再证明△FP
2P∽△FQ
2Q,求出x
1的值,根据实际情况取值.
点评:[点评]本题对学生有一定的能力要求,涉及了初中数学的大部分重点章节的重点知识,是一道选拔功能卓越的好题.

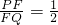 ,求直线l的解析式.
,求直线l的解析式.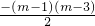 ,
, 圆心所在直线
圆心所在直线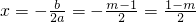 ,
,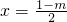 与x轴交于点D,圆心为O',
与x轴交于点D,圆心为O',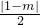 .
.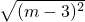 =|m-3|,BD=
=|m-3|,BD= ,
,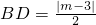 .
.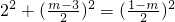 .
.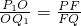 .
.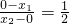 ,即x2=-2x1.
,即x2=-2x1. 则PP2∥QQ2.所以△FP2P∽△FQ2Q.
则PP2∥QQ2.所以△FP2P∽△FQ2Q.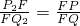 .
.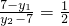 .
.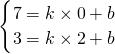 ,
,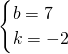
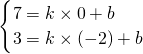 ,
,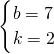


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案