
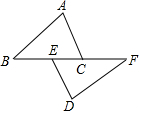
 如图,AB=DF,AC=DE,BE=FC,问:△ABC与△DEF全等吗?AB与DF平行吗?请说明你的理由.
如图,AB=DF,AC=DE,BE=FC,问:△ABC与△DEF全等吗?AB与DF平行吗?请说明你的理由.  口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
| A. | (1+40%)a元 | B. | (1-40%)a元 | C. | $\frac{a}{1+40%}$元 | D. | $\frac{a}{1-40%}$元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 互为相反数 | B. | 互为倒数 | C. | 互为有理化因式 | D. | 相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
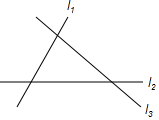 如图所示,直线l1,l2,l3表示三条相互交叉公路,现要建一个货物中转站,求它到三条公路的距离相等,则可供选择的地址共有( )处.
如图所示,直线l1,l2,l3表示三条相互交叉公路,现要建一个货物中转站,求它到三条公路的距离相等,则可供选择的地址共有( )处.| A. | 1 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:$\sqrt{2}$:$\sqrt{3}$ | B. | 1:$\sqrt{3}$:2 | C. | 1:2:3 | D. | 1:2:$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com