
| 1 |
| 1ΓΝ2 |
| 1 |
| 2 |
| 1 |
| 2ΓΝ3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3ΓΝ4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2ΓΝ4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4ΓΝ6 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 6ΓΝ8 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 8 |
| 1 |
| 1ΓΝ2 |
| 1 |
| 2ΓΝ3 |
| 1 |
| 3ΓΝ4 |
| 1 |
| 5ΓΝ6 |
| 1 |
| 1ΓΝ2 |
| 1 |
| 2ΓΝ3 |
| 1 |
| 3ΓΝ4 |
| 1 |
| n(n+1) |
| 1 |
| 1ΓΝ3 |
| 1 |
| 3ΓΝ5 |
| 1 |
| 5ΓΝ7 |
| 1 |
| (2n-1)(2n+1) |
| 49 |
| 99 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 6 |
| 5 |
| 6 |
| 1 |
| n+1 |
| n |
| n+1 |
| 1 |
| 1ΓΝ3 |
| 1 |
| 3ΓΝ5 |
| 1 |
| 5ΓΝ7 |
| 1 |
| (2n-1)(2n+1) |
| 49 |
| 99 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 49 |
| 99 |
| 1 |
| 2n+1 |
| 98 |
| 99 |
| 1 |
| 2n+1 |
| 1 |
| 99 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
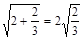 ΘΜ ΔΎ
ΘΜ ΔΎ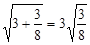 ΘΜ
ΘΜ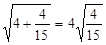 ΘΜ Δή
ΘΜ Δή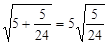
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
 Θ§
Θ§ Θ§
Θ§ Θ§
Θ§ =
= Θ®
Θ®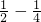 Θ©
Θ©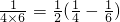
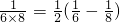
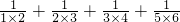 =______Θ°
=______Θ°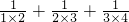 +Γ≠+
+Γ≠+ =______Θ°Θ®”ΟΚ§”–nΒΡ ΫΉ”±μ ΨΘ©
=______Θ°Θ®”ΟΚ§”–nΒΡ ΫΉ”±μ ΨΘ©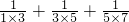 +Γ≠+
+Γ≠+ ΒΡ÷ΒΈΣ
ΒΡ÷ΒΈΣ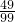 Θ§«σnΒΡΤΫΖΫΗυΘ°
Θ§«σnΒΡΤΫΖΫΗυΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚΤΎΡ©Χβ Χβ–ΆΘΚΫβ¥πΧβ
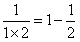
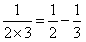
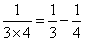
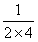 =
=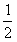 Θ®
Θ®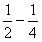 Θ©
Θ© 
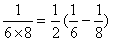
 _____ΘΜ
_____ΘΜ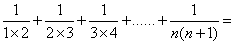 _____ Θ°Θ®”ΟΚ§”–nΒΡ ΫΉ”±μ ΨΘ©
_____ Θ°Θ®”ΟΚ§”–nΒΡ ΫΉ”±μ ΨΘ©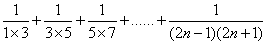 ΒΡ÷ΒΈΣ
ΒΡ÷ΒΈΣ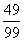 Θ§«σ
Θ§«σ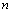 ΒΡΤΫΖΫΗυΘ°
ΒΡΤΫΖΫΗυΘ° ≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚΙψΕΪ Γ÷–ΩΦ’φΧβ Χβ–ΆΘΚΫβ¥πΧβ
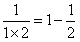
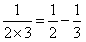
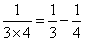
 _____ΘΜ
_____ΘΜ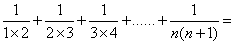 _____ ΘΜΘ®”ΟΚ§”–nΒΡ ΫΉ”±μ ΨΘ©
_____ ΘΜΘ®”ΟΚ§”–nΒΡ ΫΉ”±μ ΨΘ©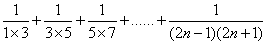 ΒΡ÷ΒΈΣ
ΒΡ÷ΒΈΣ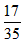 Θ§«σ
Θ§«σ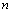 ΒΡ÷ΒΓΘ
ΒΡ÷ΒΓΘ≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com