
 如图,一个隧道的横截面成抛物线形,它的底部宽12米、高6米.车辆在此隧道可以双向通行,但规定车辆必须在隧道的中心线右侧、距离路边缘2米这一范围内行驶,并保持车辆顶部与隧道的空隙不少于
如图,一个隧道的横截面成抛物线形,它的底部宽12米、高6米.车辆在此隧道可以双向通行,但规定车辆必须在隧道的中心线右侧、距离路边缘2米这一范围内行驶,并保持车辆顶部与隧道的空隙不少于 米.
米.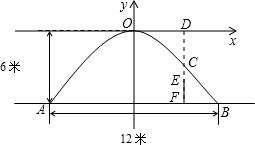
 ,
, x2 (-6≤x≤6).
x2 (-6≤x≤6). x2≥
x2≥ ,
, x2+
x2+ (-4≤x≤4,且 x≠0 ).
(-4≤x≤4,且 x≠0 ). <0,
<0, ×42+
×42+ =3,
=3, 米可得出不等式,从而得出通过隧道车辆的高度的最大值.
米可得出不等式,从而得出通过隧道车辆的高度的最大值.

科目:初中数学 来源: 题型:
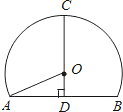 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=( )
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=( )| A、5 | ||
| B、7 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
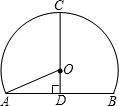 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=12米,净高CD=9米,则此圆的半径OA=( )
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=12米,净高CD=9米,则此圆的半径OA=( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一个隧道的横截面成抛物线形,它的底部宽12米、高6米.车辆在此隧道可以双向通行,但规定车辆必须在隧道的中心线右侧、距离路边缘2米这一范围内行驶,并保持车辆顶部与隧道的空隙不少于
如图,一个隧道的横截面成抛物线形,它的底部宽12米、高6米.车辆在此隧道可以双向通行,但规定车辆必须在隧道的中心线右侧、距离路边缘2米这一范围内行驶,并保持车辆顶部与隧道的空隙不少于| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源:2013年海南省海口市中考数学模拟试卷(九)(解析版) 题型:解答题
 米.
米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com