
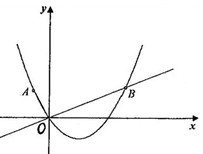
已知:直角坐标平面内有点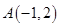 ,过原点
,过原点 的直线
的直线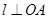 ,且与过点
,且与过点 、
、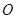 的抛物线相交于第一象限的
的抛物线相交于第一象限的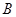 点,若
点,若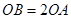 .
.
(1)求抛物线的解析式;
(2)作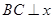 轴于点
轴于点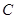 ,设有直线
,设有直线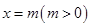 交直线
交直线 于
于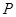 ,交抛物线于点
,交抛物线于点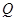 ,若
,若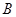 、
、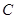 、
、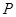 、
、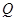 组成的四边形是平行四边形,求
组成的四边形是平行四边形,求 的值。
的值。
(1)解:过点A作AH⊥x轴于点H,过点B作BC⊥x轴于点C,
由点A(-1,2)可得 AH=2,OH=1
由直线OB⊥OA,可得△AHO∽△OCB,
∴ 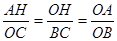 ,
,
∵OB=2OA,∴OC=4,BC=2 ,∴B(4,2)
设经过点A、O、B的抛物线解析式为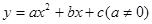
∴ 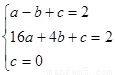 )
)
解得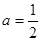 ,
,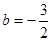 ∴抛物线解析式为:
∴抛物线解析式为: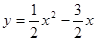
(2)设直线l的解析式为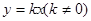
∵ 直线l经过点B(4,2), ∴ 直线l的解析式为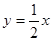
∵ 直线x=m(m>0)交直线l于,交抛物线于点Q,
∴ 设P点坐标为(m,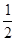 m),点Q坐标为(m,
m),点Q坐标为(m,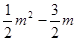 ),
),
∵由B、C、P、Q四点组成的四边形是平行四边形,∴ PQ//BC且PQ=BC
即: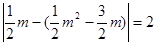 ,
,
解得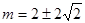 或
或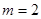 , ∵ m>0 ∴
, ∵ m>0 ∴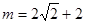 或2
或2
【解析】(1)过点A作AH⊥x轴于点H,过点B作BC⊥x轴于点C,根据点A的坐标可得出AH及OH的长度,再由△AHO∽△OCB及OB=2OA可求出点B的坐标,利用待定系数法可求出函数解析式.
(2)先求出直线l的解析式,然后根据B、C、P、Q组成的四边形是平行四边形,结合题意可得PQ=BC,建立方程求解即可得出m的值.


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
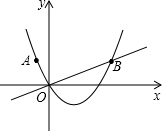 (2012•奉贤区二模)已知:直角坐标平面内有点A(-1,2),过原点O的直线l⊥OA,且与过点A、O的抛物线相交于第一象限的B点,若OB=2OA.
(2012•奉贤区二模)已知:直角坐标平面内有点A(-1,2),过原点O的直线l⊥OA,且与过点A、O的抛物线相交于第一象限的B点,若OB=2OA.查看答案和解析>>
科目:初中数学 来源: 题型:
6
| ||
| x |
| 2 |
3
| ||
| 2 |
| 2 |
3
| ||
| 2 |
6
| ||
| x |
6
| ||
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年上海市浦东新区中考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com