
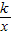 上有一点P(m,n)且m、n是关于t的一元二次方程t2-3t+k=0的两根,且P点到原点的距离为
上有一点P(m,n)且m、n是关于t的一元二次方程t2-3t+k=0的两根,且P点到原点的距离为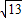 ,则双曲线的表达式为 .
,则双曲线的表达式为 . 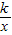 的图象上,得到mn=k;由m、n是关于t的一元二次方程t2-3t+k=0的两根,得到m+n=3,根据P点到原点的距离为
的图象上,得到mn=k;由m、n是关于t的一元二次方程t2-3t+k=0的两根,得到m+n=3,根据P点到原点的距离为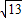 ,利用勾股定理可得m2+n2=13,将所得三个式子组成方程组即可解答.
,利用勾股定理可得m2+n2=13,将所得三个式子组成方程组即可解答.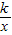 得:mn=k①;
得:mn=k①;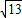 ,
, [(m+n)2-(m2+n2)]=
[(m+n)2-(m2+n2)]= ×(32-13)=-2,
×(32-13)=-2,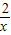 .
. .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
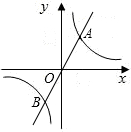 如图,已知直线y=
如图,已知直线y=
| ||
| 3 |
| k |
| x |
| 3 |
| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
| 8 |
| m |
| 1 |
| 2 |
| -8 |
| x |
 时,点A、B、C、D围成的四边形面积.
时,点A、B、C、D围成的四边形面积.查看答案和解析>>
科目:初中数学 来源: 题型:
| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
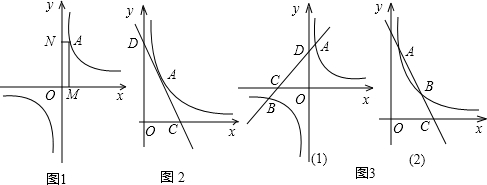
 如图,已知直线y=
如图,已知直线y= x与双曲线y=
x与双曲线y= 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为 .
. 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积; 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省江阴华士片八年级下学期期中考试数学卷(带解析) 题型:解答题
阅读理解:对于任意正实数a、b,∵( -
- )2≥0,∴a-2
)2≥0,∴a-2 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在a+b≥2 (a、b均为正实数)中,若ab为定值p,则a+b≥2
(a、b均为正实数)中,若ab为定值p,则a+b≥2 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 . 根据上述内容,回答下列问题:
. 根据上述内容,回答下列问题:
(1)若m>0,只有当m= 时,m+ 有最小值 ;
有最小值 ;
若m>0,只有当m= 时,2m+ 有最小值 .
有最小值 .
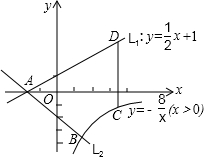
(2)如图,已知直线L1:y= x+1与x轴交于点A,过点A的另一直线L2与双曲线y=
x+1与x轴交于点A,过点A的另一直线L2与双曲线y=
(x>0)相交于点B(2,m),求直线L2的解析式.
(3)在(2)的条件下,若点C为双曲线上任意一点,作CD∥y轴交直线L1于点D,试
求当线段CD最短时,点A、B、C、D围成的四边形面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com