练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．将自然数1至2010按图中的方式排列：

    如图，用一个长方形框出9个数（3行3列），已知这9个数的和为17991，求这9个数中最小的数．

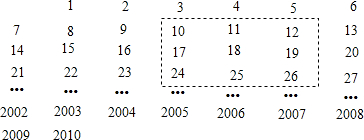
    分析 根据所给数可得长方形框出9个数，同一行的数要依次加1，同一列的数要依次加7，且长方形中第一个数最小，设第一个数为x，可依次表示这9个数为x，x+1，x+2，x+7，x+8，x+9，x+14，x+15，x+16，令它们的和为17991，列出方程，解得x．

    解答 解：设第一个数为x，则其它数依次为x+1，x+2，x+7，x+8，x+9，x+14，x+15，x+16，
    由题意得，x+x+1+x+2+x+7+x+8+x+9+x+14+x+15+x+16=17991，
    解得：x=1991，
    故这9个数中最小的数是1991．

    点评 本题主要考查了数字的变化规律，发现规律，根据题意列出方程是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．阅读下列材料，然后回答问题．在进行二次根式的化简运算时，我们有时会碰上形如$\frac{2}{\sqrt{3}+1}$的式子，其实我们还可以将其进一步简化：$\frac{2}{\sqrt{3}+1}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}+1）（\sqrt{3}-1）}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}）^{2}-{1}^{2}}$=$\sqrt{3}$-1．以上这种化简的步骤叫做分母有理化．
    请用上面的方法化简：$\frac{1}{2-\sqrt{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

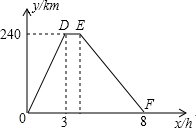    2．小王从A地前往B地送货，到达B地后，休息1h后按原路返回，他与A地的距离y（单位：km）和所用的时间x（单位；h）之间的函数关系式如图所示．
    （1）小王从B地返回A地的速度是多少？
    （2）在A，B之间有一个C地，小王从去时途径C地到返回时路过C地，公用了4.5h，那么A，C两地相距多远？
    （3）小李在小王出发2h后，按小王大的路线也从A地前往B地，行驶路程为216km/时，在小王返回途中两人相遇，问小李行驶了多长时间？直接写出结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．求一次函数y=$\frac{1}{2}$x-1的图象与一次函数y=-x-3的图象的交点坐标，并求出这两个函数的图象与x轴所围成的三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．下列函数表达式中，表示y是x的反比例函数的是④、⑤、⑥．
    ①y=3x+1；②y=0.75x；③x：y=20；④xy=-1：⑤y=5x-1；⑥y=$\frac{k}{x}$（k≠0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

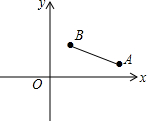    5．如图，在平面直角坐标系中，已知A（a，1），B（2，b），且a，b满足（2a-3b-2）2+$\sqrt{a-2b}$=0．
    （1）求A，B的坐标；
    （2）在y轴上是否存在点P，使S△PAB=1？若存在，直接写出满足条件的所有点P的坐标，并任选一个P点坐标，写出求解过程；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．若点P（m+1，5）在第二象限，则m＜-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．探究：中华人民共和国国旗上的五角星的每个角均相等，小明为了计算每个角的度数，画出了如图①的五角星，每个角均相等，并写出了如下不完整的计算过程，请你将过程补充完整．
    解：∵∠AFG=∠C+∠E，∠AGF=∠B+∠D．
    ∴∠AFG+∠AGF=∠C+∠E+∠B+∠D．
    ∵∠A+∠AFG+∠AGF=180°，
    ∴∠A+∠B+∠C+∠D+∠E=180°，
    ∴∠A=∠B=∠C=∠D=∠E=36°．
    拓展：如图②，小明改变了这个五角星的五个角的度数，使它们均不相等，请你帮助小明求∠A、∠B、∠C、∠D、∠E的和．
    应用：如图③．小明将图②中的点A落在BE上，点C落在BD上，若∠B=∠D=36°，则∠CAD+∠ACE+∠E=108°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．已知a＞0，b＞0，且a+b=7，则代数式$\sqrt{{x^2}+{a^2}}+\sqrt{{{（11-x）}^2}+{b^2}}$的最小值为$\sqrt{170}$．

    查看答案和解析>>

    同步练习册答案