Question

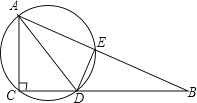
【题目】如图，在Rt△ABC中，∠ACB=90°，AD平分∠BAC，过A，C，D三点的圆与斜边AB交于点E，连接DE．

（1）求证：AC=AE；

（2）若AC=6，CB=8，求△ACD外接圆的直径．

Answer 1

【答案】（1）证明见解析；（2）3

【解析】试题分析：（1）由Rt△ABC中，∠ACB=90°，可得AD是直径，可得△ADE为直角三角形，在两个直角三角形中，利用AAS可得两三角形全等，得到答案；

（2）先根据勾股定理求出AB的长，由（1）知，AC=AE，CD=DE，设CD=x，则BD=8-x，在Rt△BDE中，根据勾股定理求出x的值，同理，在Rt∠ACD中求出AD的长，进而可得出结论．

试题解析：

（1）证明：∵Rt△ABC中，∠ACB=90°，

∴AD为圆的直径，

∴∠AED=90°，

∵AD是△BAC的∠CAB的角平分线，

∴∠CAD=∠EAD，

Rt△ACD与Rt△ADE中，

∠CAD=∠BAD， ∠ACB=∠AED ，AD=AD ，

∴Rt△ACD≌Rt△ADE（AAS），

∴AC=AE．

（2）∵在Rt△ABC中，∠ACB=90°，AC=6，CB=8，

∴

∵由（1）知，AC=AE，CD=DE，∠ACD=∠AED=90°，

∴设CD=x，则BD=8-x，BE=AB-AE=10-6=4，

在Rt△BDE中， ，即 解得x=3．

在Rt△ACD中 即解得AD=.