
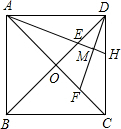
 如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.| EF |
| DC |
|

|
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| EF |
| DC |
| 2 |
| 2 |


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 型号 | A | B |
| 成本(万元/台) | 200 | 240 |
| 售价(万元/台) | 250 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)
已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com