
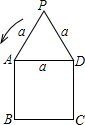
 如图,等边三角形和正方形的边长都是a,在图形所在的平面内,将△PAD以点A为中心沿逆时针方向旋转,使AP与AB重合,如此继续分别以点B、C、D 为中心将三角形进行旋转,使点P回到原来位置为止,则点P从开始到结束所经过路径的长为
如图,等边三角形和正方形的边长都是a,在图形所在的平面内,将△PAD以点A为中心沿逆时针方向旋转,使AP与AB重合,如此继续分别以点B、C、D 为中心将三角形进行旋转,使点P回到原来位置为止,则点P从开始到结束所经过路径的长为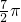 a
a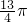 a
a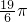 a
a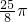 a
a 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
 次抽到纸牌上的图形都为既是中心对称图形又是轴对称图形的概率(纸牌用A、B、C表示)
次抽到纸牌上的图形都为既是中心对称图形又是轴对称图形的概率(纸牌用A、B、C表示)查看答案和解析>>
科目:初中数学 来源: 题型:044
(1)如图 (1),O为边长为a的正方形ABCD的旋转中心,现将一块半径足够大,圆心角∠EOF为90°的扇形纸板的圆心放在点O上,并让其绕点O旋转,扇形两边交正方形边上于M、N两点,则被纸覆盖的M到N之间的虚线长为______,重叠部分的面积等于______.
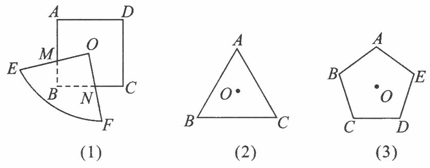
(2)如图 (2),将一块半径足够长的扇形纸板的圆心放在边长为a的等边三角形和正五边形的中心O处,并将其绕点O旋转,当扇形纸板的圆心角∠EOF为______度时,与等边三角形的覆盖部分的总长度为a;当扇形纸板的圆心角∠EOF为______度时,与正五边形的覆盖部分的总长度也为a.
(3)一般地,将一块半径足够长的扇形纸板的圆心放在边长为a的正多边形的中心O处,并将纸板绕点O旋转,当扇形纸板的圆心角∠EOF为______度时,与正多边形的覆盖部分的总长度为定值a,此时覆盖部分的面积是否也为定值?若是,那么它占整个正多边形面积的几分之几?若不是定值,请说明理由:___________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
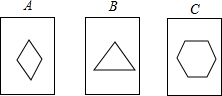
如图,现有三张质地和大小完全相同的不透明的纸牌,A、B、C,其正面画有菱形、等边三角形、正六边形,纸牌的背面完全相同,现将这三张纸牌背面朝上洗匀后随机抽出一张,再从剩下的纸牌中随机抽出一张,用画树状图或列表法,求两次抽到纸牌上的图形都为既是中心对称图形又是轴对称图形的概率(纸牌用A、B、C表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,现有三张质地和大小完全相同的不透明的纸牌,A、B、C,其正面画有菱形、等边三角形、正六边形,纸牌的背面完全相同,现将这三张纸牌背面朝上洗匀后随机抽出一张,再从剩下的纸牌中随机抽出一张,用画树状图或列表法,求两次抽到纸牌上的图形都为既是中心对称图形又是轴对称图形的概率(纸牌用A、B、C表示)
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山东济宁卷)数学 题型:解答题
如图,现有三张质地和大小完全相同的不透明的纸牌,A、B、C,其正面画有菱形、等边三角形、正六边形,纸牌的背面完全相同,现将这三张纸牌背面朝上洗匀后随机抽出一张,再从剩下的纸牌中随机抽出一张,用画树状图或列表法,求两次抽到纸牌上的图形都为既是中心对称图形又是轴对称图形的概率(纸牌用A、B、C表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com