解:(1)(3

-

)(

+2

)
=(3

-2

)(3

+2

)
=(3

)
2-(2

)
2
=18-12
=6;
(2)4(x-1)
2-9(x-5)
2=0,
变形为:[2(x-1)]
2-[3(x-5)]
2=0,
因式分解得:[2(x-1)+3(x-5)][2(x-1)-3(x-5)]=0,
(2x-2+3x-15)(2x-2-3x+15)=0,即(5x-17)(-x+13)=0,
可化为5x-17=0或-x+13=0,
解得:x
1=

,x
2=13.
分析:(1)将第一个括号中的减数化为最简二次根式,第二个括号中的第一个加数化为最简二次根式,然后利用平方差公式变形,根据平方根的定义化简后,相减即可得到最后结果;
(2)将方程左边变形后,利用平方差公式分解因式,根据两数相乘积为0,转化为两个一元一次方程,分别求出方程的解,即可得到原方程的解.
点评:此题考查了利用因式分解法求一元二次方程的解,以及二次根式的混合运算,利用分解因式法解方程时,首先将方程右边化为0,方程左边的多项式分解因式后,根据两数相乘积为0,两因式中至少有一个为0,转化为两个一元一次方程,达到降次的目的,进而求出方程的解;二次根式的加减运算关键是合并同类二次根式,合并的关键是将二次根式化为最简二次根式,二次根式的乘除运算关键是掌握法则,最后结果必须化为最简,有时可以利用平方差公式及完全平方公式来简化运算.

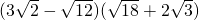
 -
- )(
)( +2
+2 )
) -2
-2 )(3
)(3 +2
+2 )
) )2-(2
)2-(2 )2
)2 ,x2=13.
,x2=13.
