2或6
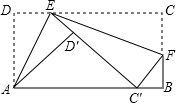
分析:设DE=x,根据翻折的性质可得∠AED=∠AEC′,∠CEF=∠C′EF,然后求出∠AED+∠CEF=90°,根据同角的余角相等求出∠DAE=∠CEF,然后求出△ADE和△ECF相似,根据相似三角形对应边成比例列式求出CF,然后表示出BF、C′D′,再根据△AC′D′和△C′FB相似列式求出BC′,然后表示出AC′,在Rt△AC′D′中,利用勾股定理列式求解即可;再根据矩形的边长,当点E为CD的中点时,C′、D′、F三点重合,为AB的中点.
解答:设DE=x,则CE=CD-DE=AB-DE=12-x,
由翻折的性质得,∠AED=∠AEC′,∠CEF=∠C′EF,
∴∠AED+∠CEF=

×180°=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠CEF,
又∵∠D=∠C=90°,
∴△ADE∽△ECF,
∴
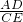
=

,
即
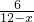
=
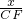
,
解得CF=
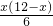
,
∴BF=BC-CF=6-
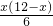
=
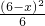
,C′D′=C′E=D′E=12-x-x=12-2x,
由翻折的性质,∠AD′C′=∠EC′F=90°,
∴AD′∥C′F,
∴∠C′AD′=∠BC′F,
又∵∠AD′C=∠B=90°,
∴
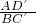
=
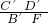
,
即
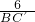
=
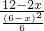
,
解得BC′=

,
∴AC′=12-

=
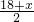
,
在Rt△AC′D′中,AD′
2+C′D′
2=AC′
2,
即6
2+(12-2x)
2=(
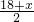
)
2,
整理得,5x
2-76x+132=0,
解得x
1=2,x
2=
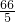
(舍去),
故,DE=2,
当点E为CD的中点时,C′、D′、F三点重合,为AB的中点,
此时DE=

×12=6,
综上所述,DE的长为2或6.
故答案为:2或6.
点评:本题考查了翻折变换的性质,主要利用了相似三角形的判定与性质,勾股定理的应用,熟记翻折前后的两个图形能够重合得到相等的线段和角是解题的关键,本题要注意点E为CD的中点的情况.

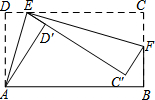 已知一个矩形纸片ABCD,AB=12,BC=6,点E为DC边上的动点(点E不与点D、C重合),经过点A、E折叠该纸片,得点D′和折痕AE,经过点E再次折叠纸片,使点C落在直线ED′上,得点C′和折痕EF.当点C′恰好落在边AB上时,DE的长为________.
已知一个矩形纸片ABCD,AB=12,BC=6,点E为DC边上的动点(点E不与点D、C重合),经过点A、E折叠该纸片,得点D′和折痕AE,经过点E再次折叠纸片,使点C落在直线ED′上,得点C′和折痕EF.当点C′恰好落在边AB上时,DE的长为________. ×180°=90°,
×180°=90°,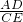 =
= ,
,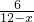 =
=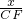 ,
,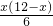 ,
,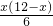 =
=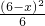 ,C′D′=C′E=D′E=12-x-x=12-2x,
,C′D′=C′E=D′E=12-x-x=12-2x,
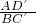 =
=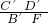 ,
,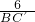 =
=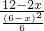 ,
, ,
, =
=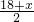 ,
,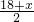 )2,
)2,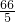 (舍去),
(舍去), ×12=6,
×12=6,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案