练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
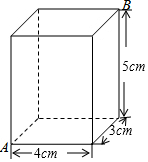
    2．图是一个长、宽、高分别为4cm，3cm，5cm的长方体，一只蚂蚁从顶点A出发，沿长方体的表面爬行至点B，爬行的最短路程是多少？

    分析 把此长方体的一面展开，在平面内，两点之间线段最短．利用勾股定理求点A和B点间的线段长，即可得到蚂蚁爬行的最短距离．在直角三角形中，一条直角边长等于长方体的高，另一条直角边长等于长方体的长宽之和，利用勾股定理可求得．

    解答 解：因为平面展开图不唯一，
    故分情况分别计算，进行大、小比较，再从各个路线中确定最短的路线．
    （1）展开前面、右面，由勾股定理得AB2=（5+4）2+32=90；
    （2）展开前面、上面，由勾股定理得AB2=（3+4）2+52=74；
    （3）展开左面、上面，由勾股定理得AB2=（3+5）2+42=80；
    所以最短路径长为$\sqrt{74}$cm．

    点评 此题是平面展开图--最短路径问题，主要考查了勾股定理的应用．“化曲面为平面”是解决“怎样爬行最近”这类问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    15．分解因式：ax2-2a2x+a3=a（x-a）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知正方形ABCD的边长为6，点P从点B出发，以每秒1个单位长度的速度沿BC边运动，点Q从C点同时出发，以相同的速度在BC的延长线上运动，当点P运动到点C时，点Q也停止运动，连接AP，过P点作AP的垂线，与过点Q垂直于BC的直线m相交于点E，连接AE交CD于点F设点P的运动时间为t秒（t＞0）
    （1）∠PAE的度数为45°，EQ=t（用t表示）；
    （2）△PCF的周长会随着t的变化而变化吗？若变化说明理由，若不变求出定值；
    （3）当△PAF为等腰三角形时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，直线y=2x与双曲线y=$\frac{k}{x}$交于点A（m，2）．
    （1）求k的值；
    （2）将直线y=2x向下平移交y轴于B，交双曲线于P，△AOP的面积为2，求直线PB的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，已知在△ABC中，∠ACB=90°，AC=BC，P为AB上一个动点，连接CP，在CP顺时针的方向，以PC为斜边作△PCE，PE=CE，∠PEC=90°，连接AE．
    （1）如图①，当∠BCP=22.5°时，求证：AE平分∠BAC；
    （2）如图②，延长AE交BC的延长线于点D，求证：AE=DE；
    （3）在（2）的条件下，连接BE，交AC于点O，若BE平分∠ABC，AC=（$\sqrt{2}$+1）CD，求$\frac{OE}{CE}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知抛物线y=x2+h与x轴交于A、B两点，与y轴交于C点，且OC=AB．
    （1）求此抛物线的解析式；
    （2）直线y=2x+b被抛物线截得线段长为2$\sqrt{30}$，求b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．定义：两组邻边财应相等的四边形为筝形
    如图，在筝形ABCD中，AB=AD=2$\sqrt{2}$，BC=CD=6，∠DAB=90°
    （1）在图1中，作一条直线将筝形ABCD的面积二等分，并说明理由．
    （2）在图2中，利用尺规在筝形ABCD中找一点P，连接PB、PD，使折线BPD将筝形ABCD的面积二等分（不写作法）．并说明理由．
    （3）在筝形ABCD中，是否存在一条过点D的直线将筝形ABCD的面积二等分？若存在，求出该筝形截这条直线所得线段的长的平方；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，双曲线y1=$\frac{{k}_{1}}{x}$（x＜0）经过A（-2，3），双曲线y2=$\frac{{k}_{2}}{x}$（x2＞0）经过C点，D点在y轴正半轴上，B（1，0）点在x轴的正半轴上，若四边形ABCD是矩形．
    （1）求双曲线y1（x＜0）的解析式；
    （2）双曲线y2（x＞0）解析式．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年湖北省武汉市侏儒山街四校七年级3月月考数学试卷（解析版） 题型：判断题

    阅读理【解析】
    计算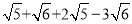时我们可以将式子中的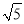、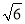分别看成两个相同的字母a、b；则原式可看成a+b+2a﹣3b，我们用类比合并同类项的方法可将上面的式子化简．

    【解析】

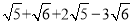
    =（1+2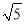）+（1-3）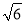

    =3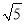﹣2

    类比以上解答方式化简： |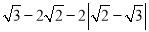

    查看答案和解析>>

    同步练习册答案