
分析 由二次函数的解析式可知,当x=1时,所对应的函数值y=t=a+b+1.把点(-1,0)代入y=ax2+bx+1,a-b+1=0,然后根据顶点在第一象限,可以画出草图并判断出a与b的符号,进而求出t=a+b+1的变化范围.
解答 解:∵二次函数y=ax2+bx+1的顶点在第一象限,
且经过点(-1,0),
∴易得:a-b+1=0,a<0,b>0,
由a=b-1<0得到b<1,结合上面b>0,所以0<b<1①,
由b=a+1>0得到a>-1,结合上面a<0,所以-1<a<0②,
∴由①+②得:-1<a+b<1,
在不等式两边同时加1得0<a+b+1<2,
∵a+b+1=t代入得0<t<2,
∴0<t<2.
故答案为:0<t<2.
点评 此题主要考查了二次函数的性质,二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特殊点的关系,也要掌握在图象上表示一元二次方程ax2+bx+c=0的解的方法.同时注意特殊点的运用.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
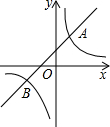 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
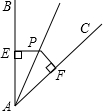 如图点P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
如图点P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )| A. | HL | B. | ASA | C. | AAS | D. | SAS |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com