Question

附加题：
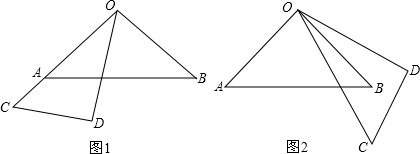
已知将一副三角板（直角三角板OAB和直角三角板OCD，∠AOB=90°，∠COD=30°）如图1摆放，点O、A、C在一条直线上．将直角三角板OCD绕点O逆时针方向转动，变化摆放如图位置
（1）如图1，当点O、A、C在同一条直线上时，∠BOD的度数是______；如图2，若要OB恰好平分∠COD，则∠AOC的度数是______．

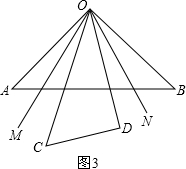
（2）如图3，当三角板OCD摆放在∠AOB内部时，作射线OM平分∠AOC，射线ON平分∠BOD，如果三角板OCD在∠AOB内绕点O任意转动，∠MON的度数是否发生变化？如果不变，求其值；如果变化，说明理由．

（3）当三角板OCD从图1的位置开始，绕点O逆时针方向旋转一周，保持射线OM平分∠AOC、射线ON平分∠BOD（∠AOC≤180°，∠BOD≤180°），在旋转过程中，（2）中的结论是否保持不变？如果保持不变，请说明理由；如果变化，请说明变化的情况和结果（即旋转角度a在什么范围内时∠MON的度数是多少）．

Answer 1

（1）∠BOD=90°-∠COD=90°-30°=60°，
∠AOC=90°-

1

2

∠COD=90°-

1

2

×30°=75°．

（2）不变，60°．
根据图中所示∠MON=

1

2

（∠AOB-∠COD）+∠COD=

1

2

（90°-30°）+30°=60度．

（3）①当0°＜α＜180°时，
∠MON=

1

2

（90°+∠BOC）+

1

2

（30°+∠BOC）-∠BOC=60°
②α=180°时，即∠AOC为平角，
（1）点M在OB上，
∴∠MOD=∠BOC+∠COD=90°+30°=120°，
又∵ON平分∠BOD，
∴∠MON=120×

1

2

=60度．
（2）点M在BO上，
∠MON=180°-60°=120度．
故∠MON=60°或120°
③180°＜α＜240°时，
2（30°+∠MOD）+90°+∠CON+（∠CON+30°）=360°，
解得：∠MOD+∠CON=90°，则
∠MON=90°+30°=120°
③当α=240°时，∠BOD=180°，那么此时N可以平分在∠BOD的左边，使得∠MON=60°，N平分在∠BOD的右边，那么∠MON=120°
⑤240°＜α＜360°时，
∠MON=

1

2

（30°-∠AOD）+

1

2

（90°-∠AOD）+∠AOD=60度．