
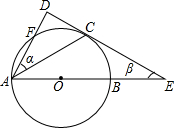
 如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作切线DE的垂线,垂足为D,且与⊙O交于点F,设∠DAC,∠CEA的度数分别是α,β.
如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作切线DE的垂线,垂足为D,且与⊙O交于点F,设∠DAC,∠CEA的度数分别是α,β.分析 (1)首先证明∠DAE=2α,在Rt△ADE中,根据两锐角互余,可知2α+β=90°,(0°<α<45°);
(2)连接OF交AC于O′,连接CF.只要证明四边形AFCO是菱形,推出△AFO是等边三角形即可解决问题;
解答 解:(1)连接OC.
∵DE是⊙O的切线,
∴OC⊥DE,
∵AD⊥DE,
∴AD∥OC,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAE=2α,
∵∠D=90°,
∴∠DAE+∠E=90°,
∴2α+β=90°(0°<α<45°).
(2)连接OF交AC于O′,连接CF.
∵AO′=CO′,
∴AC⊥OF,
∴FA=FC,
∴∠FAC=∠FCA=∠CAO,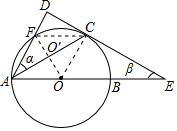
∴CF∥OA,∵AF∥OC,
∴四边形AFCO是平行四边形,
∵OA=OC,
∴四边形AFCO是菱形,
∴AF=AO=OF,
∴△AOF是等边三角形,
∴∠FAO=2α=60°,
∴α=30°,
∵2α+β=90°,
∴β=30°,
∴α=β=30°.
点评 本题考查切线的性质、垂径定理、菱形的判定.等边三角形的判定和性质等知识,等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
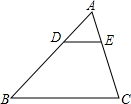 如图,在△ABC中,D、E分别为AB、AC上的点,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则$\frac{AD+DE+AE}{AB+BC+AC}$=$\frac{1}{3}$.
如图,在△ABC中,D、E分别为AB、AC上的点,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则$\frac{AD+DE+AE}{AB+BC+AC}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{-a+b}$ | B. | $\frac{a}{a+b}$ | C. | -$\frac{-a}{a-b}$ | D. | -$\frac{a}{a+b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
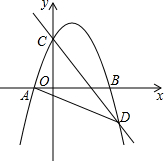 如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-$\frac{3}{2}$x+3交于C、D两点.连接BD、AD.
如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-$\frac{3}{2}$x+3交于C、D两点.连接BD、AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
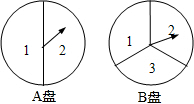 小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.
小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (m+n)(-m-n)=m2-n2 | B. | (2a-b)2=4a2-2ab+b2 | ||
| C. | (x+3)(-x+3)=x2-9 | D. | (4x+1)2=16x2+8x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com