
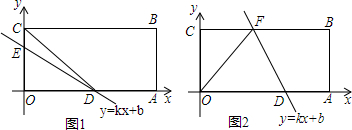
���� ��1�����ݾ��ε����ʵõ���A��C�����꣬Ȼ�����е��������õ�D�����꣬��C��D���������ֱ����ֱ��l��y=kx+b��k��0�������ڷ��������ϵ����ֵ��
��2���������ε������ʽ��֪��E�����꣬����E��D������ֱ����ֱ��l��y=kx+b��k��0�������ڷ��������ϵ����ֵ����Ҫ�������ۣ�S��DEO��S��DEC=1��2��S��DEC��S��DEO=1��2���������
��3����Ҫ�������ۣ���OF=DF��OD=OF��OD=DF��������µ�k��ֵ��
��� 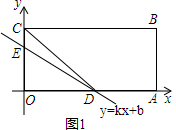 �⣺��1����ͼ1���߾���OABC���������������ϣ���B������Ϊ��10��3����
�⣺��1����ͼ1���߾���OABC���������������ϣ���B������Ϊ��10��3����
��A��10��0����C��0��3����
�֡ߵ�DΪOA���е㣬
��D��5��0����
��C��0��3����D��5��0���ֱ����y=kx+b��k��0������
$\left\{\begin{array}{l}{3=b}\\{0=5k+b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{3}{5}}\\{b=3}\end{array}\right.$��
��ֱ��l�Ľ���ʽ�Ľ���ʽΪ��y=-$\frac{3}{5}$x+3��
��2���ٵ�S��DEO��S��DEC=1��2ʱ��OE��EC=1��2����ʱE��0��1����
��E��0��1����D��5��0���ֱ����y=kx+b��k��0������
$\left\{\begin{array}{l}{1=b}\\{0=5k+b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{1}{5}}\\{b=1}\end{array}\right.$��
��ֱ��l�Ľ���ʽ�Ľ���ʽΪ��y=-$\frac{1}{5}$x+1��
�ڵ�S��DEC��S��DEO=1��2ʱ��OE��EC=2��1����ʱE��0��2����
��E��0��2����D��5��0���ֱ����y=kx+b��k��0������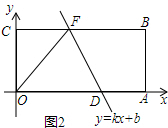
$\left\{\begin{array}{l}{2=b}\\{0=5k+b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{2}{5}}\\{b=2}\end{array}\right.$��
��ֱ��l�Ľ���ʽ�Ľ���ʽΪ��y=-$\frac{2}{5}$x+2��
����������ֱ��l�Ľ���ʽ�Ľ���ʽΪ��y=-$\frac{1}{5}$x+1��y=-$\frac{2}{5}$x+2��
��3����ͼ2��
�ٵ�OF=DFʱ����F���߶�OD���д����ϣ���ʱF��2.5��3����
��D��5��0����F��2.5��3���ֱ����y=kx+b��k��0������
$\left\{\begin{array}{l}{0=5k+b}\\{3=2.5k+b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{6}{5}}\\ b=\frac{6}{25}}\end{array}\right.$��
�ڵ�OD=OF=5ʱ�����ݹ��ɶ�����CF=4����F��4��3����
��D��5��0����F��4��3���ֱ����y=kx+b��k��0������
$\left\{\begin{array}{l}{0=5k+b}\\{3=4k+b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-{3}}\\ b={15}}\end{array}\right.$��
�۵�OD=DF=5ʱ�����ݹ��ɶ�����F��1��3����
��D��5��0����F��1��3���ֱ����y=kx+b��k��0������
$\left\{\begin{array}{l}{0=5k+b}\\{3=k+b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{15}{4}}\end{array}\right.$��
����������k��ֵ��-$\frac{6}{5}$��-3��-$\frac{3}{4}$��
���� ������Ҫ�����˾��ε����ʣ����������ε������Լ�һ�κ������ۺ�Ӧ�ã������ڶ�������ʱ��Ҫ�Զ��������IJ�ͬλ�ý��з������ۣ��Է�©�⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 6 | B�� | 5 | C�� | 3 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
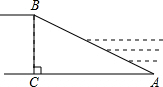 ��ͼ���ӵ̺����ӭˮ��AB���Ʊ���$1��\sqrt{3}$���̸�BC=12cm��������AB�ij����ǣ�������
��ͼ���ӵ̺����ӭˮ��AB���Ʊ���$1��\sqrt{3}$���̸�BC=12cm��������AB�ij����ǣ�������| A�� | 15cm | B�� | $20\sqrt{3}$cm | C�� | 24cm | D�� | $10\sqrt{3}$cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
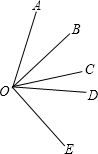 ��ͼ��ʾ����֪0Bƽ�֡�AOC��ODƽ�֡�BOE����BOE=90�㣬��BOC=2��COD�����A0E�Ķ�����
��ͼ��ʾ����֪0Bƽ�֡�AOC��ODƽ�֡�BOE����BOE=90�㣬��BOC=2��COD�����A0E�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
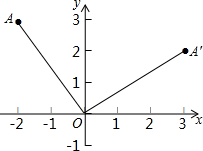 ��ͼ����A����Ϊ��-2��3��������A��ԭ��O˳ʱ����ת90��õ�A�䣬��A������꣮
��ͼ����A����Ϊ��-2��3��������A��ԭ��O˳ʱ����ת90��õ�A�䣬��A������꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
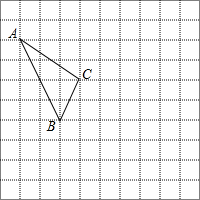 ��ͼ���������������У�ÿ��С�����εı߳�Ϊ1������ABC�Ķ���A��C������ֱ�Ϊ��-4��5������-1��3��
��ͼ���������������У�ÿ��С�����εı߳�Ϊ1������ABC�Ķ���A��C������ֱ�Ϊ��-4��5������-1��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com