
��2011•���ݣ���ƽ��ֱ������ϵXOY�У�ֱ��l1����A��1��0������y��ƽ�У�ֱ��l2����B��0��2������x��ƽ�У�ֱ��l1��ֱ��l2�ཻ�ڵ�P����EΪֱ��l2��һ�㣬����������![]() ��k��0����ͼ�����E��ֱ��l1�ཻ�ڵ�F��
��k��0����ͼ�����E��ֱ��l1�ཻ�ڵ�F��
��1������E���P�غϣ���k��ֵ��
��2������OE��OF��EF����k��2���ҡ�OEF�����Ϊ��PEF�������2������E������ꣻ
��3���Ƿ���ڵ�E��y���ϵĵ�M��ʹ���Ե�M��E��FΪ��������������PEFȫ�ȣ������ڣ���E�����ꣻ�������ڣ���˵�����ɣ�

�⣺��1������E���D�غϣ���k=1��2=2��
��2����k��2ʱ����ͼ1����E��F�ֱ���P����Ҳ���Ϸ�����E��x��Ĵ���EC������ΪC����F��y��Ĵ���FD������ΪD��EC��FD�ཻ�ڵ�G�����ı���OCGDΪ���Σ�
��PF��PE��
��S��FPE=![]() PE•PF=
PE•PF=![]() ��
��![]() ��1����k��2��=
��1����k��2��=![]() k2��k+1��
k2��k+1��
���ı���PFGE�Ǿ��Σ�
��S��PFE=S��GEF��
��S��OEF=S����OCGD��S��DOF��S��EGD��S��OCE=![]() •k����
•k����![]() k2��k+1����k=
k2��k+1����k=![]() k2��1
k2��1
��S��OEF=2S��PEF��
��![]() k2��1=2��
k2��1=2��![]() k2��k+1����
k2��k+1����
���k=6��k=2��
��k=2ʱ��E��F�غϣ�
��k=6��
��E����������3��2����
��3�����ڵ�E��y���ϵĵ�M��ʹ�á�MEF�ա�PEF��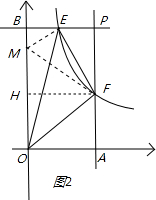
�ٵ�k��2ʱ����ͼ2��ֻ�����ǡ�MEF�ա�PEF����FH��y����H��
�ߡ�FHM�ס�MBE��
��![]() =
=![]() ��
��
��FH=1��EM=PE=1��![]() ��FM=PF=2��k��
��FM=PF=2��k��
��![]() =
=![]() ��BM=
��BM=![]() ��
��
��Rt��MBE�У��ɹ��ɶ����ã�EM2=EB2+MB2��
�ࣨ1��![]() ��2=��
��2=��![]() ��2+��
��2+��![]() ��2��
��2��
���k=![]() ����ʱE������Ϊ��
����ʱE������Ϊ��![]() ��2����
��2����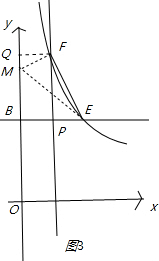
�ڵ�k��2ʱ����ͼ3��ֻ�����ǡ�MFE�ա�PEF����FQ��y����Q����FQM�ס�MBE�ã�![]() =
=![]() ��
��
��FQ=1��EM=PF=k��2��FM=PE=![]() ��1��
��1��
��![]() =
=![]() ��BM=2��
��BM=2��
��Rt��MBE�У��ɹ��ɶ����ã�EM2=EB2+MB2��
�ࣨk��2��2=��![]() ��2+22�����k=
��2+22�����k=![]() ��0����k=0���������⣬
��0����k=0���������⣬
��k=![]() ��
��
��ʱE������Ϊ��![]() ��2����
��2����
�����������E��������![]() ��2����
��2����![]() ��2����
��2����

����:��


 ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��2011•���ʣ���һ�ξ��꼶ѧ����������У���������8���˵�����������������£�4.0��4.2��4.5��4.0��4.4��4.5��4.0��4.8��������˵������ȷ���ǣ�������
A���������ݵ���λ����4.4 B���������ݵ�������4.5
C���������ݵ�ƽ������4.3 D���������ݵļ�����0.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011���������������п���ѧ�����Ծ��������棩 ���ͣ�ѡ����
��2011•�����أ�Ŀǰ��ȫ��ˮ��Դ������٣��ᳫȫ����Լ��ˮ���ݲ��ԣ�š������ˮ��ͷÿ���ӵγ�100��ˮ��ÿ��ˮԼ0.05������С��ͬѧϴ�ֺ�û�а�ˮ��ͷš����ˮ��ͷ�Բ��Ե��ٶȵ�ˮ����С���뿪x���Ӻ�ˮ��ͷ�γ�y������ˮ����д��y��x֮��ĺ�����ϵʽ�ǣ�������
A��y=0.05x B��y=5x
C��y=100x D��y=0.05x+100
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�����ʡ���꼶��ѧ�����п�����ѧ�� ���ͣ�ѡ����
��2011•��������ͼ����DEF����������ƽ�Ƶõ���ABC��������
A���ѡ�DEF����ƽ��4����λ��������ƽ��2����λ
B���ѡ�DEF����ƽ��4����λ��������ƽ��2����λ
C���ѡ�DEF����ƽ��4����λ��������ƽ��2����λ
D���ѡ�DEF����ƽ��4����λ��������ƽ��2����λ[��Դ:Z+xx+k.Com]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�꽭��ʡ�������п���ѧ�Ծ� ���ͣ������
��2011•���ݣ���֪����ͼ���ڡ�ABC�У�DΪBC�ϵ�һ�㣬ADƽ�֡�EDC���ҡ�E=��B��DE=DC����֤��AB=AC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�꽭��ʡ�������п���ѧ�Ծ� ���ͣ������
��2011•���ݣ�ij��2007��5�·�ijһ�ܵ���������£���λ���棩�ֱ�Ϊ��25��28��30��29��31��32��28�����ܵ���������µ�ƽ��ֵ�ǡ棬��λ���������森
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com