
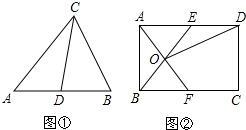
���� Ӧ�ã���1������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ��õ��ı���ABFE��ƽ���ı��Σ�Ȼ�����ƽ���ı��ε�����֤��OE=OB������֤�á�AOE�͡�AOB���Ѻ������Σ�
��2����AOE�͡�DOE�ǡ��Ѻ������Ρ������ɵõ�E��AD���е㣬�������á�ABE����ABF�����������S�ı���CDOF=S����ABCD-2S��ABF������⣮
̽���������������������������������ı���A��DCB��ƽ���ı��Σ����BC��A��D�Ƴ���ACB=90�㣬���������������ʽ������ɣ��������CQ�������A��DC����������������ABC�����
��� Ӧ�ã���1��֤�������ı���ABCD�Ǿ��Σ�
��AD��BC��
��AE=BF��
���ı���ABFE��ƽ���ı��Σ�
��OE=OB��
���AOE�͡�AOB���Ѻ������Σ�
��2���⣺�ߡ�AOE�͡�DOE���Ѻ������Σ�
��S��AOE=S��DOE��AE=ED=$\frac{1}{2}$AD=3��
�ߡ�AOB���AOE���Ѻ������Σ�
��S��AOB=S��AOE��
�ߡ�AOE�ա�FOB��
��S��AOE=S��FOB��
��S��AOD=S��ABF��
��S�ı���CDOF=S����ABCD-2S��ABF=4��6-2��$\frac{1}{2}$��4��3=12��
̽����
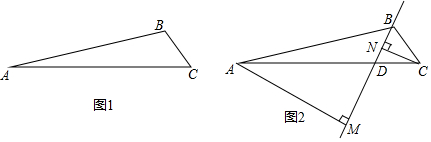
�⣺��Ϊ�������������ͼ1��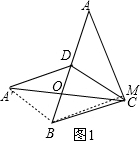
��S��ACD=S��BCD��
��AD=BD=$\frac{1}{2}$AB=4��
����CD�۵�A��A���غϣ�
��AD=A��D=$\frac{1}{2}$AB=$\frac{1}{2}$��8=4��
�ߡ�A��CD���ABC�غϲ��ֵ�������ڡ�ABC�����$\frac{1}{4}$��
��S��DOC=$\frac{1}{4}$S��ABC=$\frac{1}{2}$S��BDC=$\frac{1}{2}$S��ADC=$\frac{1}{2}$S��A��DC��
��DO=OB��A��O=CO��
���ı���A��DCB��ƽ���ı��Σ�
��BC=A��D=4��
��B��BM��AC��M��
��AB=8����BAC=30�㣬
��BM=$\frac{1}{2}$AB=4=BC��
��C��M�غϣ�
���ACB=90�㣬
�ɹ��ɶ����ã�AC=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$��
���ABC�������$\frac{1}{2}$��BC��AC=$\frac{1}{2}$��4��4$\sqrt{3}$=8$\sqrt{3}$��
����ͼ2��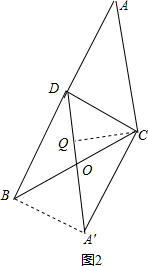
��S��ACD=S��BCD��
��AD=BD=$\frac{1}{2}$AB��
����CD�۵�A��A���غϣ�
��AD=A��D=$\frac{1}{2}$AB=$\frac{1}{2}$��8=4��
�ߡ�A��CD���ABC�غϲ��ֵ�������ڡ�ABC�����$\frac{1}{4}$��
��S��DOC=$\frac{1}{4}$S��ABC=$\frac{1}{2}$S��BDC=$\frac{1}{2}$S��ADC=$\frac{1}{2}$S��A��DC��
��DO=OA�䣬BO=CO��
���ı���A��BDC��ƽ���ı��Σ�
��A��C=BD=4��
��C��CQ��A��D��Q��
��A��C=4����DA��C=��BAC=30�㣬
��CQ=$\frac{1}{2}$A��C=2��
��S��ABC=2S��ADC=2S��A��DC=2��$\frac{1}{2}$��A��D��CQ=2��$\frac{1}{2}$��4��2=8��
����ABC�������8��8$\sqrt{3}$��
���� �����Ǽ��α任�ۺ��⣬��Ҫ������ƽ���ı������ʺ��ж��������ε���������ɶ�����Ӧ�ã��������Ĺؼ����ܸ�����֪�������ѧ�Ķ���������������Ŀ�ȽϺã�������һ�����Ѷȣ�


 ������ϵ�д�
������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
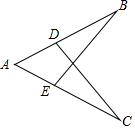 ��1����ͼ����֪��B=��C��AD=AE����֤��BD=CE��
��1����ͼ����֪��B=��C��AD=AE����֤��BD=CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
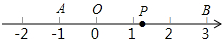 ��֪����������A��B��Ӧ�����ֱ�Ϊ-1��3����PΪ������һ���㣬���Ӧ����ΪX��
��֪����������A��B��Ӧ�����ֱ�Ϊ-1��3����PΪ������һ���㣬���Ӧ����ΪX���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com