解:(1)令x=0,y=-2,
当y=0代入y=

x-2得出:x=4,
故B,C的坐标分别为:
B(4,0),C(0,-2).
y=

x
2-

x-2.
(2)△ABC是直角三角形.
证明:令y=0,则

x
2-

x-2=0.
∴x
1=-1,x
2=4.
∴A(-1,0).
解法一:∵AB=5,AC=

,BC=2

.
∴AC
2+BC
2=5+20=25=AB
2.
∴△ABC是直角三角形.
解法二:∵AO=1,CO=2,BO=4,
∴

∵∠AOC=∠COB=90°,
∴△AOC∽△COB.
∴∠ACO=∠CBO.
∵∠CBO+∠BCO=90°,
∴∠ACO+∠BCO=90度.
即∠ACB=90度.
∴△ABC是直角三角形.
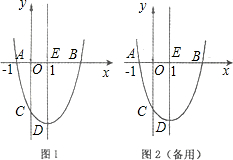
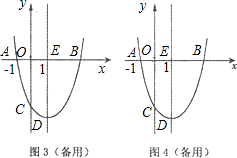
(3)能.①当矩形两个顶点在AB上时,如图1,CO交GF于H.

∵GF∥AB,
∴△CGF∽△CAB.
∴

.
解法一:设GF=x,则DE=x,
CH=

x,DG=OH=OC-CH=2-

x.
∴S
矩形DEFG=x•(2-

x)=-

x
2+2x=-

(x-

)
2+

.
当x=

时,S最大.
∴DE=

,DG=1.
∵△ADG∽△AOC,
∴

,
∴AD=

,
∴OD=

,OE=2.
∴D(-

,0),E(2,0).
解法二:设DG=x,则DE=GF=

.
∴S
矩形DEFG=x•

=-

x
2+5x=-

(x-1)
2+

.
∴当x=1时,S最大.
∴DG=1,DE=

.
∵△ADG∽△AOC,
∴

,
∴AD=

,
∴OD=

,OE=2.
∴D(-

,0),E(2,0).
②当矩形一个顶点在AB上时,F与C重合,如图2,
∵DG∥BC,
∴△AGD∽△ACB.
∴

.

解法一:设GD=x,
∴AC=

,BC=2

,
∴GF=AC-AG=

-

.
∴S
矩形DEFG=x•(

-

)=-

x
2+

x
=-

(x-

)
2+

.
当x=

时,S最大.∴GD=

,AG=

,
∴AD=

.
∴OD=

∴D(

,0)
解法二:设DE=x,

∵AC=

,BC=2

,
∴GC=x,AG=

-x.
∴GD=2

-2x.
∴S
矩形DEFG=x•(2

-2x)=-2x
2+2

x=-2(x-

)
2+

∴当x=

时,S最大,
∴GD=

,AG=

.
∴AD=

.
∴OD=

∴D(

,0)
综上所述:当矩形两个顶点在AB上时,坐标分别为(-

,0),(2,0)
当矩形一个顶点在AB上时,坐标为(

,0).
分析:(1)令x=0以及y=0代入y=

x-2得出B,C的坐标.把相关坐标代入抛物线可得函数关系式.
(2)已知AB,AC,BC的值,根据反勾股定理可证明△ABC是直角三角形.
(3)证明△CGF∽△CAB,利用线段比求出有关线段的值.求出S
矩形DEFG的最大值.再根据△ADG∽△AOC的线段比求解.
点评:本题考查的是二次函数的综合运用以及三角形相似的判定,考生要学会灵活运用二次函数的相关知识.

 x2+bx+c与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是y=
x2+bx+c与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是y= x-2,连接AC.
x-2,连接AC.
 x-2得出:x=4,
x-2得出:x=4, x2-
x2- x-2.
x-2. x2-
x2- x-2=0.
x-2=0. ,BC=2
,BC=2 .
.

 .
. x,DG=OH=OC-CH=2-
x,DG=OH=OC-CH=2- x.
x. x)=-
x)=- x2+2x=-
x2+2x=- (x-
(x- )2+
)2+ .
. 时,S最大.
时,S最大. ,DG=1.
,DG=1. ,
, ,
, ,OE=2.
,OE=2. ,0),E(2,0).
,0),E(2,0). .
. =-
=- x2+5x=-
x2+5x=- (x-1)2+
(x-1)2+ .
. .
. ,
, ,
, ,OE=2.
,OE=2. ,0),E(2,0).
,0),E(2,0). .
.
 ,BC=2
,BC=2 ,
, -
- .
. -
- )=-
)=- x2+
x2+ x
x (x-
(x- )2+
)2+ .
. 时,S最大.∴GD=
时,S最大.∴GD= ,AG=
,AG= ,
, .
. ∴D(
∴D( ,0)
,0)
 ,BC=2
,BC=2 ,
, -x.
-x. -2x.
-2x. -2x)=-2x2+2
-2x)=-2x2+2 x=-2(x-
x=-2(x- )2+
)2+
 时,S最大,
时,S最大, ,AG=
,AG= .
. .
.
 ,0)
,0) ,0),(2,0)
,0),(2,0) ,0).
,0). x-2得出B,C的坐标.把相关坐标代入抛物线可得函数关系式.
x-2得出B,C的坐标.把相关坐标代入抛物线可得函数关系式.

 阅读快车系列答案
阅读快车系列答案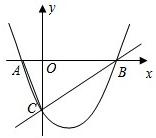 如图1,已知:抛物线y=
如图1,已知:抛物线y=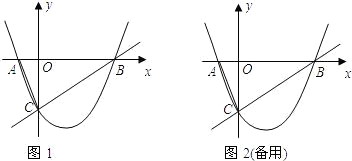

 与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是
与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是 ,连结AC.
,连结AC.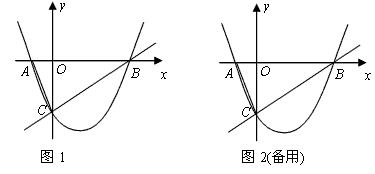
 的顶点坐标是
的顶点坐标是 ]
]