
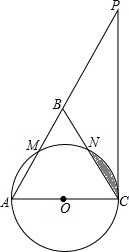
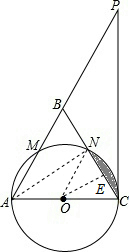
 (2013•鄂尔多斯)如图,△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(2013•鄂尔多斯)如图,△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| OE |
| OC |
| OE | ||
2
|
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
60π×(2
| ||
| 360 |
| 3 |


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
 (2013•鄂尔多斯)中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型(如图所示)摆出相同姿势,才能穿墙而过,否则会被推入水池.若墙上的三个空洞恰是某个几何体的三视图,则该几何体为( )
(2013•鄂尔多斯)中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型(如图所示)摆出相同姿势,才能穿墙而过,否则会被推入水池.若墙上的三个空洞恰是某个几何体的三视图,则该几何体为( )查看答案和解析>>
科目:初中数学 来源: 题型:
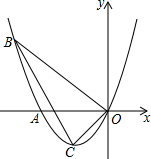 (2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.
(2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com