
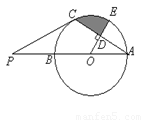
如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,连结AC,过点O作AC的垂线
交AC于点D,交⊙O于点E.已知AB﹦8,∠P=30°.
(1) 求线段PC的长;(2)求阴影部分的面积.
(1)连结OC
∵ PC切⊙O于点C ∴ 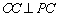
∵  ∴
∴
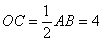
∵ 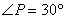 ∴
∴
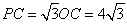
(2)∵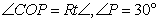 , ∴
, ∴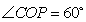 ,
,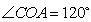
∵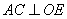 ∴
∴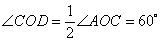 ∴
∴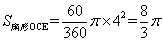
∵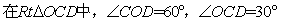
∴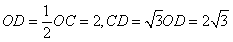 ∴
∴
∴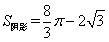
【解析】(1)连接OC,由PC为圆O的切线,根据切线的性质得到OC与PC垂直,可得三角形OCP为直角
三角形,同时由直径AB的长求出半径OC的长,根据锐角三角函数定义得到tanP为∠P的对边OC与邻边
PC的比值,根据∠P的度数,利用特殊角的三角函数值求出tanP的值,由tanP及OC的值,可得出PC的
长;
(2)由直角三角形中∠P的度数,根据直角三角形的两个锐角互余求出∠AOC的度数,进而得出∠BOC的
度数,由OD与BC垂直,且OC=OB,利用等腰三角形的三线合一得到OD为∠BOC的平分线,可求出∠
COD度数为60°,再根据直角三角形中两锐角互余求出∠OCD度数为30°,根据30°角所对的直角边等于
斜边的一半,由斜边OC的长求出OD的长,先由∠COD的度数及半径OC的长,利用扇形的面积公式求出扇
形COE的面积,再由OD与CD的长,利用直角三角形两直角边乘积的一半求出直角三角形COD的面积,用
扇形COE的面积减去三角形COD的面积,即可求出阴影部分的面积.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
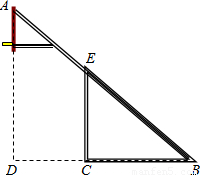
 红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)
红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)查看答案和解析>>
科目:初中数学 来源:2012届北京市石景山区九年级上学期期末考试数学卷 题型:填空题
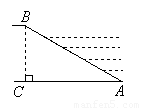
如图,是河堤的横断面,堤高BC=5米,迎水坡AB的坡比1: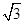 (坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是
米.
(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是
米.
查看答案和解析>>
科目:初中数学 来源:河北省模拟题 题型:解答题
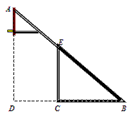
 )
) 
查看答案和解析>>
科目:初中数学 来源:2012年安徽省中考数学模拟试卷(一)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com