
Ϊ������������Ⱥ�ڵ���������ij�̳��ƻ��ڽ��ꡰ��һ�ƽ��ܡ��ڼ䣬��160000Ԫ����һ���ҵ磬�����ҵ�Ľ��ۺ��ۼ����±���
|
��� |
�ʵ� |
���� |
ϴ�»� |
|
���� |
2000 |
1600 |
1000 |
|
�ۼ� |
2200 |
1800 |
1100 |
��1����ȫ���ʽ���������ʵ��ϴ�»���100̨�����̵���Թ���ʵ��ϴ�»�������̨?
��2�����������ʽ�160000Ԫ�����ķ�Χ�ڣ������ϱ�������ҵ繲100̨�����вʵ�̨���ͱ���̨����ͬ���ҹ���ϴ�»���̨������������ʵ��̨����������һ���м��ֽ������������ֽ���������ʹ�̵������������ҵ���õ����������������������=�ۼ�-���ۣ�
��1���ʵ�60̨��ϴ�»�40̨����2���������ֽ�����������a=37ʱ��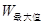 =17400
=17400
���������⣺��1�����̵깺��ʵ�x̨������ϴ�»���100��x��̨��
�����⣬��2000x+1000��100��x��=160000�� ��������������������2��
���x=60��
��100��x=40��̨����
���ԣ��̵���Թ���ʵ�60̨��ϴ�»�40̨�� ��������������.4��
��2���蹺��ʵ�ͱ����ą������ϴ�»�Ϊ��100��2a��̨��
�������⣬��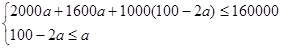 ��������.6��
��������.6��
���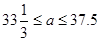 ����Ϊa������������a=34��35��36��37��
����Ϊa������������a=34��35��36��37��
��ˣ��������ֽ��������� ������������������������������������.9��
���̵�������Ϻ��õ�����ΪWԪ��
��W=��2200��2000��a+��1800��1600��a+��1100��1000����100��2a����
=200a+10000 ������������������������������������������������.10��
�൱a=37ʱ��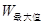 =200��37+10000=17400�� ���������������� ��.11��
=200��37+10000=17400�� ���������������� ��.11��
���ԣ��̵��õ��������Ϊ17400Ԫ����������������������������.12��
��1�����̵깺��ʵ�x̨������ϴ�»���100��x��̨�������⣬��2000x+1000��100��x��=160000,���н��
��2���蹺��ʵ�ą�����ݲʵ�������̨����ͬ������ҵ繲100̨���ֱ��ʾ�����估ϴ�»���̨�������ݱ��������ּҵ�Ľ��۱�ʾ���ּҵ���ܽ��ۣ�С�ڵ���160000Ԫ�г�����a�IJ���ʽ��ͬʱ���ݹ���ϴ�»���̨������������ʵ��̨���г���һ������a�IJ���ʽ������������ʽ��ɲ���ʽ�飬�������ʽ��⼯�е����������м������ɵó��м��ַ���������һ�κ���x��ϵ������0���õ���һ�κ���Ϊ���������ѵ�һ����x�����ֵ���뺯������ʽ�����ֵΪW�����ֵ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com