
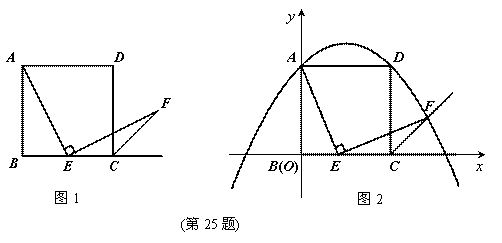
如图1,已知正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,
上,
若![]() 90°,且
90°,且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() 。
。
(1)图1中若点![]() 是边
是边![]() 的中点,我们可以构造两个三角形全等来证明
的中点,我们可以构造两个三角形全等来证明![]() ,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);(3分)
,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);(3分)
(2)如图2,若点![]() 在线段
在线段![]() 上滑动(不与点
上滑动(不与点![]() ,
,![]() 重合)。
重合)。
①![]() 是否总成立?请给出证明;(5分)
是否总成立?请给出证明;(5分)
②在如图所示的直角坐标系中,当点![]() 滑动到某处时,点
滑动到某处时,点![]() 恰好落在抛物线
恰好落在抛物线![]() 上,求此时点
上,求此时点![]() 的坐标.(4分)
的坐标.(4分)

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

| 17 |
| 17 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com