
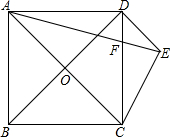
 正方形ABCD的对角线交于点O,过顶点D作AC的平行线,在这条线上取一点E,连接AE,CE,使AE=AC,AE交CD于F.则下列结论:
正方形ABCD的对角线交于点O,过顶点D作AC的平行线,在这条线上取一点E,连接AE,CE,使AE=AC,AE交CD于F.则下列结论: ;⑤
;⑤
 倍求出AC的长度,再求出AG、GE然后求出CG,然后在Rt△CEG中,利用勾股定理列式求出CE的长,判断④正确;根据FC=EC求出DF,再根据相似三角形面积的比等于相似比的平方列式计算即可得解,从而判断⑤正确.
倍求出AC的长度,再求出AG、GE然后求出CG,然后在Rt△CEG中,利用勾股定理列式求出CE的长,判断④正确;根据FC=EC求出DF,再根据相似三角形面积的比等于相似比的平方列式计算即可得解,从而判断⑤正确. (180°-30°)=75°,故②正确,
(180°-30°)=75°,故②正确,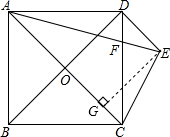
 AB=
AB= ,
, AE=
AE= ×
× =
= ,
,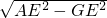 =
=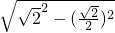 =
= ,
, -
- ,
,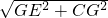 =
=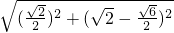 =
=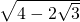 =
=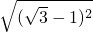 =
= -1,故④正确;
-1,故④正确; -1,
-1, -1)=2-
-1)=2- ,
,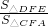 =(
=( )2=(
)2=(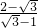 )2=
)2=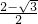 ,故⑤正确,
,故⑤正确,

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
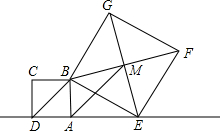 如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.
如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 如图,正方形ABCD的对角AC,BD交于点O,则结论①AB=BC=CD=DA;②AO=BO=CO=DO;③AC⊥BD中正确的有
如图,正方形ABCD的对角AC,BD交于点O,则结论①AB=BC=CD=DA;②AO=BO=CO=DO;③AC⊥BD中正确的有查看答案和解析>>
科目:初中数学 来源:2002年湖北省宜昌市中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《四边形》(01)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com