

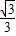 x,进而表示出AD长,在Rt△ACD中,利用∠A=30°且tan30°=
x,进而表示出AD长,在Rt△ACD中,利用∠A=30°且tan30°=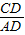 即列方程可得
即列方程可得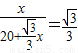 ,解方程即可.
,解方程即可.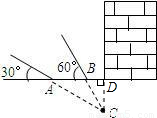 解:(1)过C作AB延长线的垂线CD,垂足为D,则CD即为所求;
解:(1)过C作AB延长线的垂线CD,垂足为D,则CD即为所求; ,
,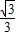 x,
x, x,
x,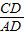 ,
,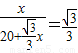 ,
,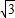 .
. 米.
米.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
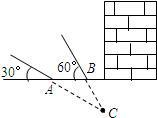 的A,B两处,用仪器探测文物C,探测线与地面的夹角分别是30°和60°(如图所示).
的A,B两处,用仪器探测文物C,探测线与地面的夹角分别是30°和60°(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:
 在玉树地震抢救中,某武警部队探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距5米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(结果取准确值).
在玉树地震抢救中,某武警部队探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距5米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(结果取准确值).查看答案和解析>>
科目:初中数学 来源: 题型:
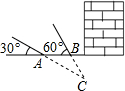
 文物探测队探测出某建筑物下面有地下文物,为了准确测出文物所在的深度,他们在文物上方建筑物的一侧地面上相距20米的A、B两处,用仪器测文物C,探测线与地面的夹角分别是30°和60°,求该文物所在位置的深度(精确到0.1米).
文物探测队探测出某建筑物下面有地下文物,为了准确测出文物所在的深度,他们在文物上方建筑物的一侧地面上相距20米的A、B两处,用仪器测文物C,探测线与地面的夹角分别是30°和60°,求该文物所在位置的深度(精确到0.1米).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北师大版九年级(上)期末数学试卷(十六)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com