解:(1)∵81
7-27
9-9
13=3
28-3
27-3
26=3
26(9-3-1)=45×3
24,
∴81
7-27
9-9
13能被45整除;
(2)反证法:假设2(2n+1)能表示为两个整数的平方差即2(2n+1)=a
2-b
2=(a+b)(a-b),
因为2(2n+1)是偶数,则a+b、a-b定有一个是偶数,
若a+b是偶数,则a、b具有相同的奇偶性,则a-b也是偶数;
同样的,若a-b偶,则a+b也偶,
则(a+b)(a-b)能被4整除也就是说2(2n+1)能被4整除,
即 2n+1能被2整除,但这是显然不成立的,
故原假设不成立,
∴当n为自然数时,2(2n+1)的形式的数不能表示为两个整数的平方差;
(3)∵

=

=

=

∴原式=

=2×(

)
=221.
分析:(1)首先将81
7-27
9-9
13代数式转化成底数为3的幂,提取公因式3
26,此时出现差5,再将3
26分解成3
24与9的乘积,问题得解;
(2)直接证明较难,因而采用反证法.假设2(2n+1)能表示为两个整数的平方差2(2n+1)=a
2-b
2.再分别就a+b、a-b是偶数
讨论,与其已知相反;
(3)观察
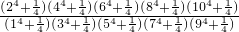
式子,发现规律:均包含有

的形式,因而对其进行因式分解得

.将此规律运用到原式中,通过对分子、分母约分化简,最后求出原式的值.
点评:本题考查因式分解的应用.解决(1)的关键是将原式通过因式分解转化为9×5×3
n的形式;(2)的关键是采用反证法;(3)的关键得到

=

这一规律,运用规律代入原式约分化简求值.

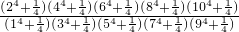 .
. =
= =
= =
=
 =2×(
=2×( )
)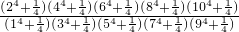 式子,发现规律:均包含有
式子,发现规律:均包含有 的形式,因而对其进行因式分解得
的形式,因而对其进行因式分解得 .将此规律运用到原式中,通过对分子、分母约分化简,最后求出原式的值.
.将此规律运用到原式中,通过对分子、分母约分化简,最后求出原式的值. =
= 这一规律,运用规律代入原式约分化简求值.
这一规律,运用规律代入原式约分化简求值. 

 阅读快车系列答案
阅读快车系列答案