
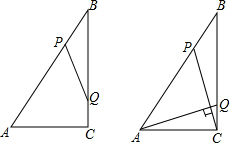
 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.分析 (1)分两种情况讨论:①当△BPQ∽△BAC时,$\frac{BP}{BA}=\frac{BQ}{BC}$,②当△BPQ∽△BCA时,$\frac{BP}{BC}=\frac{BQ}{BA}$,再根据BP=5t,QC=4t,AB=10cm,BC=8cm,代入计算即可;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,根据△ACQ∽△CMP,得出$\frac{AQ}{CP}$=$\frac{CQ}{MP}$,即可;
(3)作PE⊥AC于点E,DF⊥AC于点F,先得出DF=$\frac{PE+QC}{2}$,再把QC=4t,PE=8-BM=8-4t代入求出DF,过BC的中点R作直线平行于AC,得出RC=DF,D在过R的中位线上,从而证出PQ的中点在△ABC的一条中位线上
解答 解:(1)在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,
∴AB=10cm,
由运动知,BP=5t,QC=4t,
①当△BPQ∽△BAC时,
∵$\frac{BP}{BA}=\frac{BQ}{BC}$,
∴$\frac{5t}{10}=\frac{8-4t}{8}$,
∴t=1;
②当△BPQ∽△BCA时,
∵$\frac{BP}{BC}=\frac{BQ}{BA}$,
∴$\frac{5t}{8}=\frac{8-4t}{10}$,
∴t=$\frac{32}{41}$,
∴t=1或$\frac{32}{41}$时,△BPQ与△ABC相似;
(2)如图1所示,在Rt△ABC中,sinB=$\frac{AC}{AB}=\frac{3}{5}$, 过P作PM⊥BC于点M,AQ,CP交于点N,
过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=5t,PM=PBsinB=3t,
由运动知,CQ=4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴$\frac{AQ}{CP}=\frac{CQ}{PM}$=$\frac{4t}{3t}$=$\frac{4}{3}$;
(3)如图,作PM⊥BC于点M,PQ的中点设为D点,作PE⊥AC于点E,DF⊥AC于点F,
∵∠ACB=90°,
∴DF为梯形PECQ的中位线,
∴DF=$\frac{PE+QC}{2}$,
∵QC=4t,PE=BC-BM=8-BM=8-4t,
∴DF=$\frac{8-4t+4t}{2}$=4,
∵BC=8,
过BC的中点R作直线平行于AC,
∴RC=DF=4成立,
∴D在过R的中位线上,
∴PQ的中点在△ABC的一条中位线上.
点评 此题是相似三角形综合题,主要考查了相似三角形的判定与性质、中位线的性质等,关键是画出图形作出辅助线构造相似三角形,注意分两种情况讨论.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $0.2\stackrel{•}3$ | B. | -π | C. | $\root{3}{-8}$ | D. | $\frac{22}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有理数,a、b在数轴上的位置如图所示,则a、b、-b、-a的大小关系是( )
有理数,a、b在数轴上的位置如图所示,则a、b、-b、-a的大小关系是( )| A. | b<-a<a<-b | B. | b<a<-b<-a | C. | b<-b<-a<a | D. | b<a<-a<-b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com