
分析 (1)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)两边开方,即可得出两个一元一次方程,求出方程的解即可;
(3)先分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)(x+4)2=5(x+4),
(x+4)2-5(x+4)=0,
(x+4)(x+4-5)=0,
x+4=0,x+4-5=0,
x1=-4,x2=1;
(2)两边开方得:3x-2=±(2x-3),
解得:x1=-1,x2=1;
(3)x2-2x-8=0,
(x-4)(x+2)=0,
x-4=0,x+2=0,
x1=4,x2=-2.
点评 本题考查了解一元二次方程,能选择适当的方法解一元二次方程是解此题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
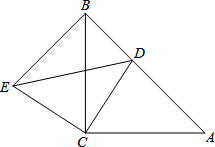 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上,连接BE.
如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一张直角三角形纸片ABC,∠C=90°,AB=24,tanB=$\frac{2}{3}$(如图),将它折叠使直角顶点C与斜边AB的中点重合,那么折痕的长为13.
一张直角三角形纸片ABC,∠C=90°,AB=24,tanB=$\frac{2}{3}$(如图),将它折叠使直角顶点C与斜边AB的中点重合,那么折痕的长为13.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com