
分析 在?ABCD中,AB<BC,要使△AB′D是直角三角形,有两种情况:∠B′AD=90°或∠AB′D=90°,画出图形,分类讨论即可.
解答 解:当∠B′AD=90°AB<BC时,如图1,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AD∥BC,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2$\sqrt{3}$,
∴∠AB′C=30°,
∴GC=$\frac{1}{2}$ B′C=$\frac{1}{2}$ BC,
∴G是BC的中点,
在Rt△ABG中,BG=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$×2$\sqrt{3}$=3,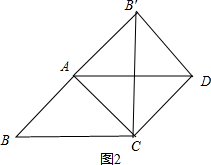
∴BC=6;
当∠AB′D=90°时,如图2,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵由折叠的性质:∠BAC=90°,
∴AC∥B′D,
∴四边形ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2$\sqrt{3}$,
∴BC=AB÷$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$×$\frac{2}{\sqrt{3}}$=4,
∴当BC的长为4或6时,△AB′D是直角三角形.
故答案为:4或6.
点评 本题主要考查了翻折变换的性质,解题的关键是画出图形,发现存在两种情况,进行分类讨论.


科目:初中数学 来源: 题型:选择题
| A. | (a-b)2=a2-b2 | B. | 3ab-ab=2ab | C. | a(a2-a)=a2 | D. | $\root{3}{8}=2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (4,-3) | B. | (-4,3) | C. | (0,-3) | D. | (0,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批圆珠笔的寿命 | |
| B. | 了解全国九年级学生身高的现状 | |
| C. | 考察人们保护海洋的意识 | |
| D. | 检查一枚用于发射卫星的运载火箭的各零部件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
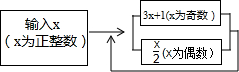 在数学活动课上,同学们利用如图的程序进行计算,发现无论x取任何正整数,结果都会进入循环,下面选项一定不是该循环的是( )
在数学活动课上,同学们利用如图的程序进行计算,发现无论x取任何正整数,结果都会进入循环,下面选项一定不是该循环的是( )| A. | 4,2,1 | B. | 2,1,4 | C. | 1,4,2 | D. | 2,4,1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com