
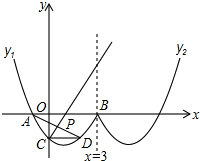
 ��ͼ���ơ�w���ĺ�������������y1��һ���֣������ʽΪ��y1=$\frac{\sqrt{3}}{3}$��x2-2x-3����x��3���Լ�������y2��һ���������ɵģ���������y2������y1����ֱ��x=3�Գƣ�A��B������y1��x�������㣨A��B����ߣ���C������y1��y�ύ�㣮
��ͼ���ơ�w���ĺ�������������y1��һ���֣������ʽΪ��y1=$\frac{\sqrt{3}}{3}$��x2-2x-3����x��3���Լ�������y2��һ���������ɵģ���������y2������y1����ֱ��x=3�Գƣ�A��B������y1��x�������㣨A��B����ߣ���C������y1��y�ύ�㣮���� ��1�������C��y2��x��Ľ������꣬���ɴ���ϵ�����������y2����ʽ���ɣ�
��2����ȷ������P�������CP�Ľ���ʽ���Ӷ����M��ĺ����꣮
��� �⣺��1����y1=$\frac{\sqrt{3}}{3}$��x2-2x-3���У�
��y1=0������$\frac{\sqrt{3}}{3}$��x2-2x-3��=0��
���x=-1��x=3��
��A��-1��0����B��3��0����
��CΪ����y1��y��Ľ��㣬
��C��0��-$\sqrt{3}$����
�֡�����y1������y2����ֱ��x=3�Գƣ�
������y2��x������������ֱ�Ϊ��3��0���루7��0����
��y2=$\frac{\sqrt{3}}{3}$��x-3����x-7��=$\frac{\sqrt{3}}{3}$��x2-10x+21������x��3��
��2����ͼ��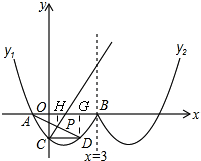
����D��DG��x�ᣬ����P��PH��x�ᣬ
��PH=$\frac{1}{2}$DG=$\frac{\sqrt{3}}{2}$��AH=$\frac{1}{2}$AG=$\frac{3}{2}$��
��OH=AH-AO=$\frac{1}{2}$��
��P��$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$����
�����߶�AD�Ĵ�ֱƽ����CP�Ľ���ʽΪy=kx+m��
�ߵ�C��0��-$\sqrt{3}$����
��$\left\{\begin{array}{l}{\frac{k}{2}+m=\frac{\sqrt{3}}{2}}\\{m=-\sqrt{3}}\end{array}\right.$��
��$\left\{\begin{array}{l}{k=\sqrt{3}}\\{m=-\sqrt{3}}\end{array}\right.$��
��CP�Ľ���ʽΪy=$\sqrt{3}$x-$\sqrt{3}$��
��y2=$\frac{\sqrt{3}}{3}$��x2-10x+21�����x=$\frac{13+\sqrt{73}}{2}$��x=$\frac{13-\sqrt{73}}{2}$���ᣬ��x��3����
��xM=$\frac{13+\sqrt{73}}{2}$��
���� �����Ƕ��κ����ۺ��⣬��Ҫ������ȷ�������Ľ������꣬�ʹ���ϵ����ȷ����������ʽ����������ʽ�ǽⱾ��Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
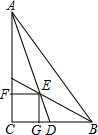 ��ͼ����Rt��ABC�У���C=90�㣬��BAC=40�㣬AD�ǡ�ABC��һ����ƽ���ߣ���E��F��G�ֱ���AD��AC��BC�ϣ����ı���CGEF�������Σ����DEB�Ķ���Ϊ��������
��ͼ����Rt��ABC�У���C=90�㣬��BAC=40�㣬AD�ǡ�ABC��һ����ƽ���ߣ���E��F��G�ֱ���AD��AC��BC�ϣ����ı���CGEF�������Σ����DEB�Ķ���Ϊ��������| A�� | 40�� | B�� | 45�� | C�� | 50�� | D�� | 55�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
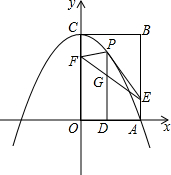 ��ͼ���߳�Ϊ8��������OABC���������������ϣ��Ե�CΪ����������߾�����A����P���������ϵ�A��C���һ�����㣨���˵㣩������P��PD��OA�ڵ�D����E��8��2����F��0��6��������PE��PF��EF��
��ͼ���߳�Ϊ8��������OABC���������������ϣ��Ե�CΪ����������߾�����A����P���������ϵ�A��C���һ�����㣨���˵㣩������P��PD��OA�ڵ�D����E��8��2����F��0��6��������PE��PF��EF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
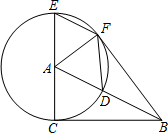 ��ͼ����֪��A�İ뾶Ϊ4��EC��Բ��ֱ������B�ǡ�A������CB�ϵ�һ�����㣬����AB����A�ڵ�D����EFƽ����AB������DF��AF��
��ͼ����֪��A�İ뾶Ϊ4��EC��Բ��ֱ������B�ǡ�A������CB�ϵ�һ�����㣬����AB����A�ڵ�D����EFƽ����AB������DF��AF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
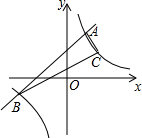 ��֪һ�κ���y1=x+5��ͼ���뷴��������y2=$\frac{k}{x}$��ͼ����A��B���㣬��֪��A�ĺ�����Ϊ1��
��֪һ�κ���y1=x+5��ͼ���뷴��������y2=$\frac{k}{x}$��ͼ����A��B���㣬��֪��A�ĺ�����Ϊ1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABCD�У�AD��BC��FΪAD���е㣬����BF���ӳ���CD���ӳ��߽��ڵ�E���ҡ�ABE=��ACE��
��ͼ����ABCD�У�AD��BC��FΪAD���е㣬����BF���ӳ���CD���ӳ��߽��ڵ�E���ҡ�ABE=��ACE���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com